多径噪声
一、 实验目的
1、熟悉无线信道多径效应产生原因及基本特性;
2、了解信道噪声的基本特性。
二、 实验原理
1、多径效应产生的原因
电磁波在传输过程中受到周围地形地物的作用将会发生反射、绕射和散射。
反射:反射发生于地球、建筑物的表面,当电磁波遇到比其波长大得多的物体时就会发生反射。
绕射:当接收机和发射机之间的无线路径被尖锐的边缘阻挡时会发生绕射。绕射产生波的弯曲,使得电磁波可以传播到阻挡体的背面。
散射:散射波产生于粗糙的表面、小物体或其他不规则物体。
由于环境对电磁波传输的影响,当电磁波传输到移动台的天线时,信号不是从单一路径而来,而是许多路径的多个信号叠加,这就是多径效应。一般来说在四种传播方式中,存在视距路径时,直射波能量最强,是接收信号中最主要的部分;反射波和绕射波能量较低,是造成多径效应的主要因素;散射波的能量小。电磁波通过的各个路径长度不同,所以各个路径电磁波到达接收机的时间不同,幅度不同,相位也不同。不同相位的多个信号在接收端叠加,有时是同相叠加而增强,有的是反相叠加而减弱。这样接收信号的幅度将会急剧变化,产生了所谓的多径衰弱。
2、多径效应的基本特性
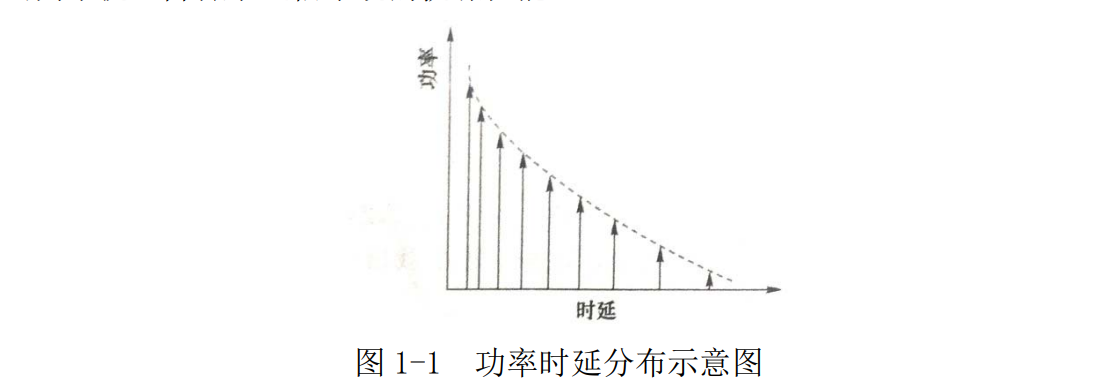
多径效应的基本特性表现在信号幅度的衰弱和时延扩展。
从空间上来说,与慢衰落不同,多径效应表现为接收信号的幅度随着移动台移动位置变化而剧烈变动。多径效应快速衰落的特性使得在较小区域内在某些位置的信号处于深衰落,信号强度急剧下降,甚至低于接收机的灵敏度,无法正常通信。
从时间上来说,由于信号的传播路径不同,当基站发出一个脉冲信号时,接收信号不仅包含该脉冲,还将包括此脉冲的各个多径时延信号,这种由于多径效应引起的接收信号中脉冲的宽度扩展现象称为时延扩展。时延扩展的存在引起了码间串扰,降低了通信系统的抗噪性能。
3、信道的噪声
对于接收端来说,不仅有多径造成的干扰,噪声也是一个不可忽略的因素。通常主要是电子器件产生的热噪声,而热噪声的特性可以用一种称为高斯白噪声的随机过程来描述。这时的信道模型称为加性高斯白噪声信道(additive white Gaussian noise channel,AWGN)。
4、两径信道分析
为了分析问题清晰,先考虑两径的情况。图 1-2 表示的是两条路径信道模型的情况。
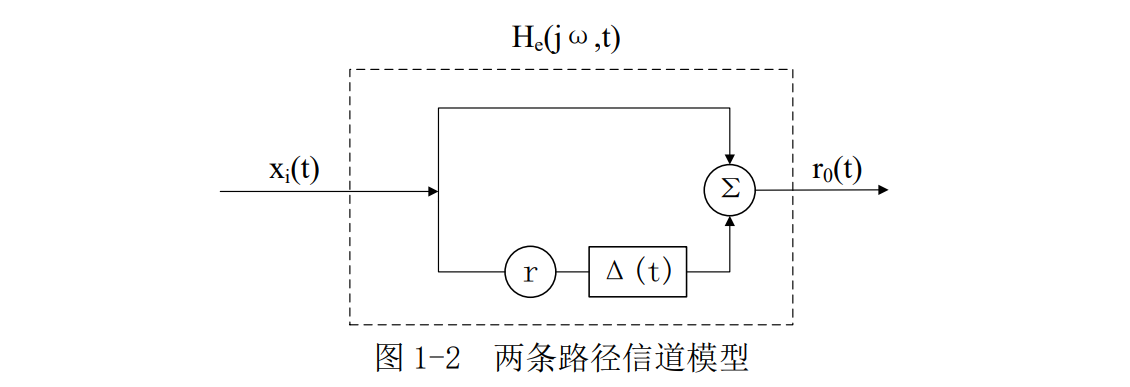
输入信号x_i(t)为实信号,第二条路径信号为Re\{rx_i(t)e^{jw\Delta(t)}\},其中r为比例
常数,\Delta(t)为两径的时延差。
r_0(t)=Re\{x_i(t)+rx_i(t-\Delta t)e^{jw\Delta(t)}\}


三、 实验仪器设备与材料
信号波形图
眼图
随机 M 进制脉冲序列模块
多径干扰模块
加性高斯白噪声信道模块
四、 实验方法与步骤要求
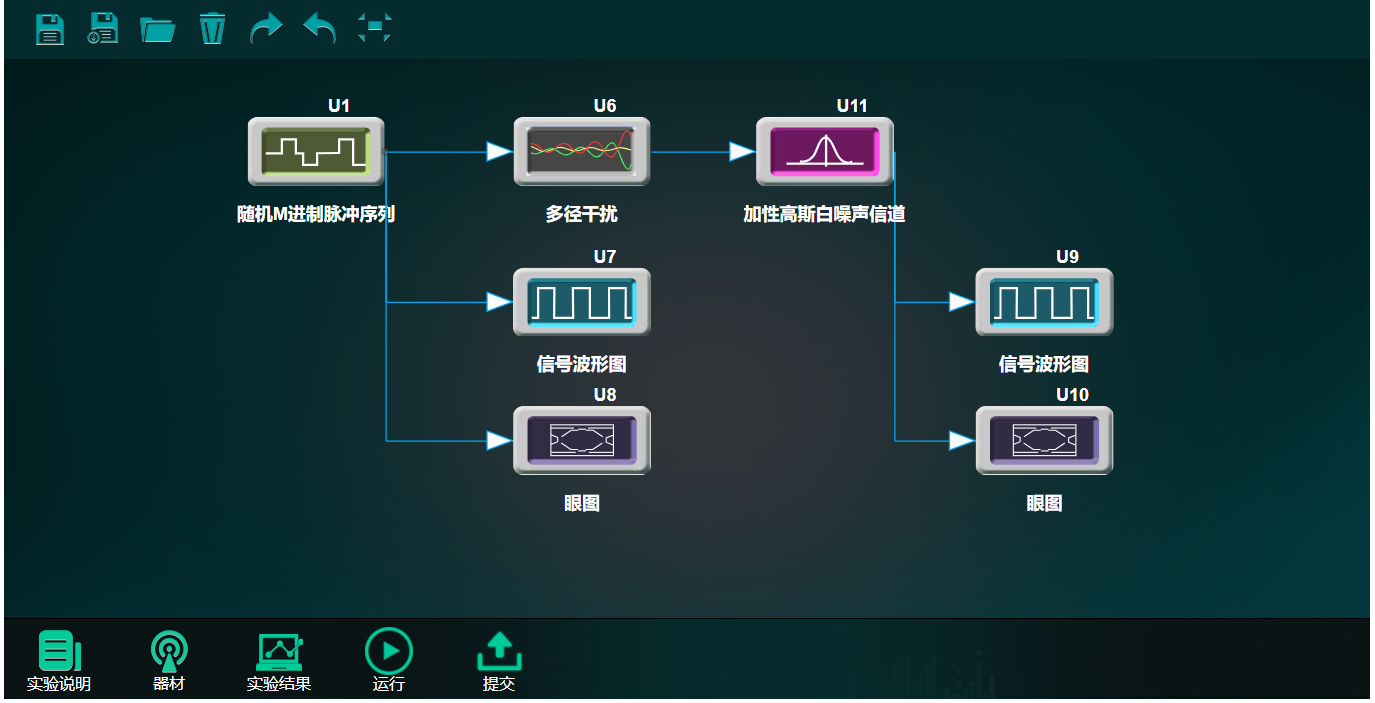
1、如图 1-4 所示搭建仿真实验模型:将随机 M 进制脉冲序列产生的伪随机序列通过两径信道和加性高斯白噪声信道,仿真对比多径干扰后的信号的波形图及眼图变化。
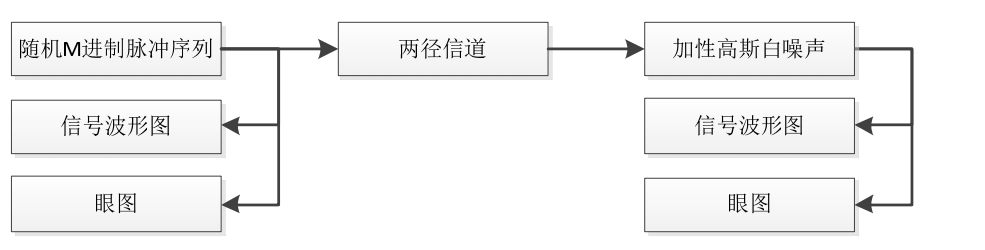
图 1-4 多径效应仿真实验模型
点击器材按钮打开“器材栏”,在“器材栏”点击模块图标,再在“工作区”点击放置模块。按照连接线方向次序左键点击连接模块和仪器,构成系统框图如下所示:
2、根据实验理论基础部分的公式 1-5 设计两径信道并写出其单位冲击响应。例如,假设码元速率为 1Mbaud/s,基带采样率为 9MHz,比例系数r为 0.5,载波频率f_c为 4GHz,多径时延\Delta t为 2/9us。
(1)设式 1-5 中s(t-\Delta t)的系数为 a,由采样率和多径时延可知,第二径信号滞后主径信号 2 个采样周期到达,信道单位冲激响应为h={1,0,a};
(2)计算系数a=rcos(2\pi f_c \Delta t)=0.383。
所以信道的单位冲激响应为h= \{1,0,0.383\}。
3、设置模块参数:(关于模块使用方法可以参考模块说明)
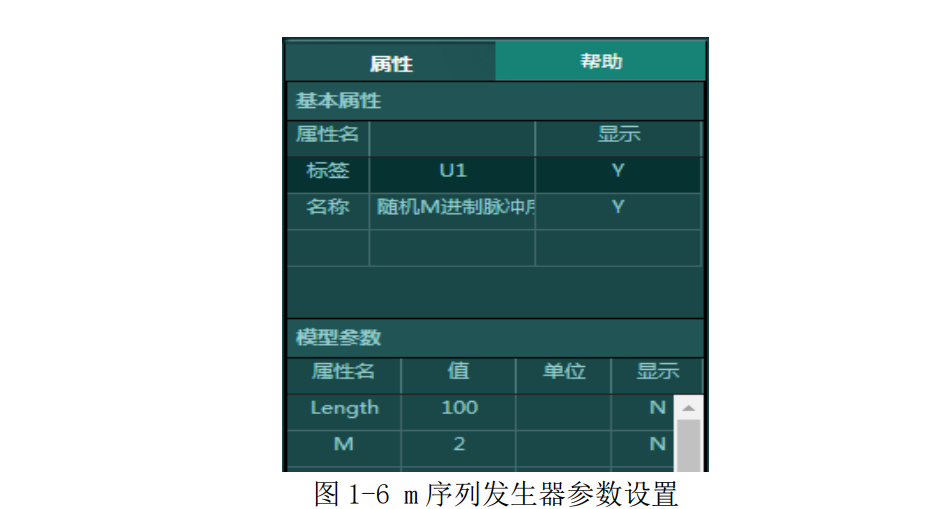
a.随机 M 进制脉冲序列模块:数据序列的长度(Length)设置为 100,进制数
(M)设置为 2;
b.多径干扰模块:将步骤 2 计算出的单位冲激响应[1 0 0.383]填入多径参数(Multipaths)。

c.加性高斯白噪声信道:信噪比(SNR)设置为 16dB

图 1-8 加性高斯白噪声信道设置
3、点击按钮打开输出栏,点击按钮运行仿真实验,观察输出波形。
4、设置多径时延\Delta t为 1/3us,其他参数不变,重新计算信道冲激响应并运行仿真实验,观察现象变化。
此时多径时延\Delta t为 1/3us,载波频率f_c为4GHz,则计算系数a=rcos(2\pi f_c \Delta t)=-0.25,所以信道的单位冲激响应为h= \{1,0,-0.25\}。
5、设置多径时延\Delta t为 2/9us,载波频率为 3GHz,重新计算信道冲激响应并运行仿真实验,观察现象变化。
此时多径时延\Delta t为 2/9us,载波频率f_c为3GHz,则计算系数a=rcos(2\pi f_c \Delta t)=-0.25,所以信道的单位冲激响应为h= \{1,0,-0.25\}。
五、 实验结果与结论
实验结果及分析:采用上述设置的参数,运行多径效应仿真实验模型,得到通
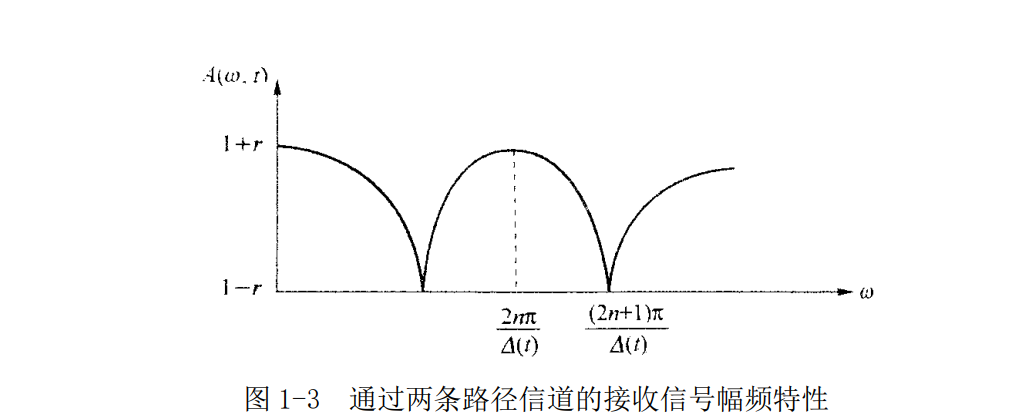
过两径信道前后的信号波形图如图 1-9、图 1-10 ,图 1-11和图1-12 所示,前后的眼图如图 1-13 ,图 1-14,图1-15和图1-16 所示。由仿真结果易知,不同的路径延迟对接收信号的幅度产生了不同的影响。当\Delta t=1/3us 时相互抵消信号使眼图张开度变小,通信误码率增大;当\Delta t=2/9us时相互叠加信号使眼图张开度变大,误码率变小。
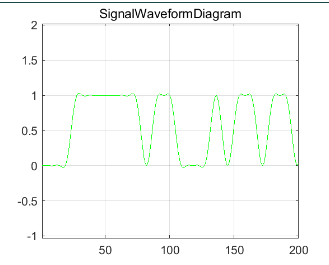
图 1-9 发端信号波形图
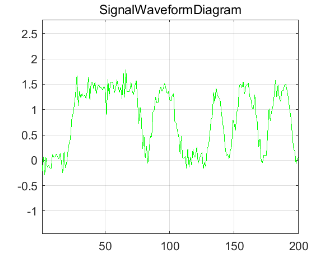
图 1-10 通过两径信道(\Delta t=2/9us,f_c=4GHz)后收端信号波形图
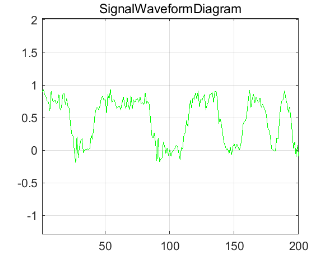
图 1-11 通过两径信道(\Delta t=1/3us,f_c=4GHz)后收端信号波形图
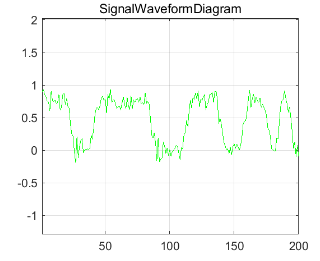
图 1-12 通过两径信道(\Delta t=2/9us,f_c=3GHz)后收端信号波形图
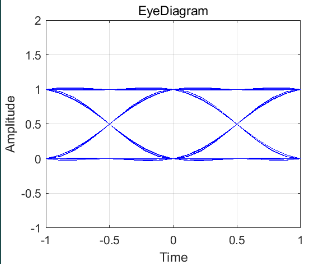
图 1-13 发端眼图
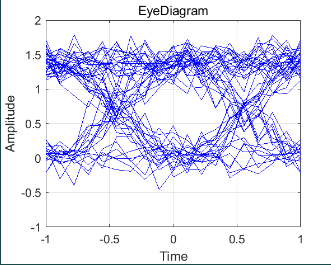
图 1-14 通过两径信道(\Delta t=2/9us,f_c=4GHz)后收端眼图
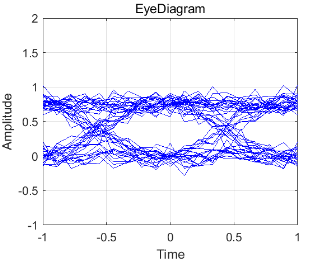
图 1-15 通过两径信道(\Delta t=1/3us,f_c=4GHz)后收端眼图
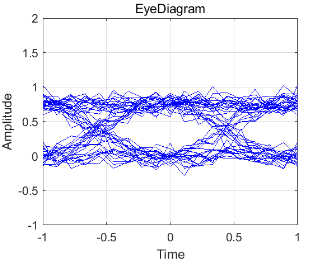
图 1-16 通过两径信道(\Delta t=2/9us,f_c=3GHz)后收端眼图


