通信原理学习——基本数字频带传输
数字频带传输
在实际通信当中,许多重要的通信信道都是带通型的,数字频带传输技术是在带通信道上传输数字信号的方法。
由发送端产生ASK、FSK或PSK信号的过程是调制,由接收端由ASK、FSK或PSK恢复出数字符号的过程是解调。
基本要点:1.确定基带信号m(t),包括基带信号的极性、几元、归零 2.确定载波,包括载波的幅度、频率、相位 3.确定基带信号与载波之间的关系,包括相乘、相加
BASK
概念:
BASK或2ASK(二进制幅移键控):通过键控(改变)正弦载波的振幅来传输0或1符号,也称为OOK
表达式:
调制方法:
由单极性二元基带信号与载波相乘得到, s_{BASK}(t)=Am(t)cos2\pi f_ct
解调方法:
包络检波——最常用的方法
接收系统包含三个基本单元:带通滤波器,包络检波器,抽样判决器
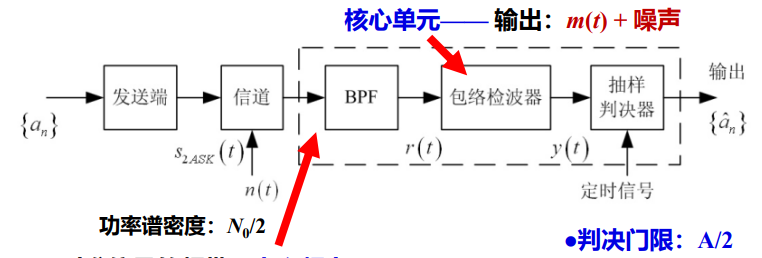
功率谱:
相应m(t)的功率谱平移到±f处,并且载波频率处存在冲激。(因为m(t)为单极性NRZ信号)
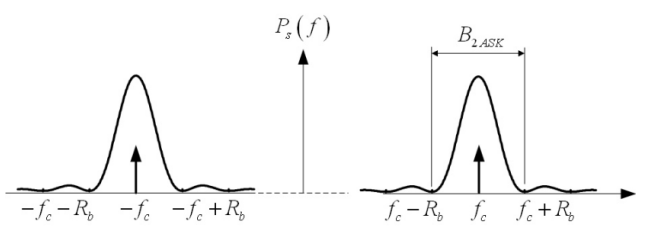
带宽:
基带信号m(t)带宽的2倍,B_{2ASK}=2B
如果基带信号m(t)是NRZ方波信号: B=1/T_b=R_b, 所以: B_{2ASK}=2R_b
理论上,二元基带信号最小带宽为R_b/2,因此2ASK最小带宽为B_{2ASK}=R_b
误码性能分析:
P_e \approx \frac{1}{2}e^{-\frac{\gamma}{4}}
可将\gamma折算成\frac{E_0}{N_0},
\gamma =\frac{A^2}{2N_0B_{BPF}}=\frac{E_b}{N_0} \times \frac{2R_b}{B_{BPF}}
\gamma与BPF的带宽密切相关,B_{BPF}越小,P_e也越小;
当B_{BPF}=R_b(最小理论值)时:
包络检波系统的误码率(误码率计算公式仅适用于解调器输入信噪比足够大的情况):
P_e \approx \frac{1}{2}e^{-\frac{E_0}{2N_0}}
2ASK的平均比特能量:
E_b= \frac{\int_0^{T_b}{(Acos2\pi f_ct)^2}\,dt+0}{2}=\frac{A^2T_b}{4}
包络检波系统存在门限效应:当\frac{E_0}{N_0} 低于一定的门限值后,P_e 会迅速恶化,系统无法工作。
例题:


对比两道题,结果不同的原因在于:B_{BPF}选取的值不同!(前者选用理论最小值)
BFSK
概念:
二进制频移键控,键控正弦载波的频率来传输二元信号
表达式:
调制方法:
s_{2FSK}(t)=Am(t)cos2\pi f_1t+A\overline{m(t)}cos2\pi f_0t ,其中\overline{m(t)}=1-m(t)
所以2FSK信号可以看作两路互补的2ASK信号的叠加,过程如下:
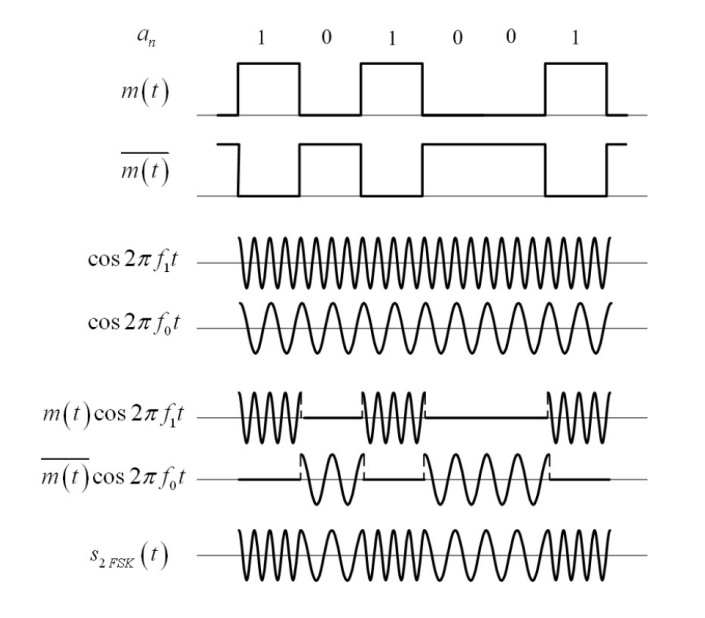
于是,产生的2FSK信号有可能“相位不连续”——在1与0码转换时,两个正弦波的连接处可能出现中断。
所以,一般需要合理选择T_b, f_1 和 f_0 的取值,可以保证相位的连续性,如:f_1=(k+1)R_b, f_0=kR_b,k为正整数
解调方法:
两种最常用的方法(都是非相干解调法):包络检波法,以及过零检测法
包络检波解调方法:
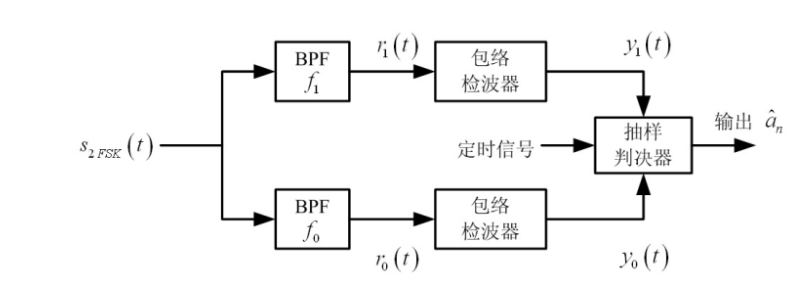
功率谱:
P_{2FSK}(f)=\frac{A^2}{4}[P_m(f+f_1)+P_m(f-f_1)+P_m(f+f_0)+P_m(f-f_0)]
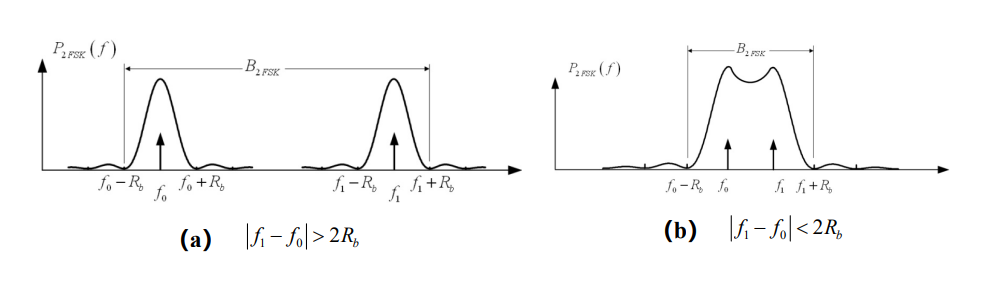
带宽:
2FSK信号带宽的定义: 两个频率峰值外侧第一个零点之间的距离
B_{2FSK}=|f_1-f_0|+2B其中:B 为基带信号带宽
要保持两个2ASK频谱基本分离,两个频率之间的距离至少为: |f_1-f_0|\geq B
例:对于矩形NRZ基带信号:B=R_b ,所以,B_{2FSK}\geq 3R_b
对于二元基带信号最小带宽为R_b/2,f_1和 f_0 的理论最小间距是||f_1-f_0|\geq \frac{R_b}{2},所以,最小带宽B_{2FSK}= 1.5R_b
f_1和 f_0 过于接近时,功率谱中两个2ASK频谱将发生重叠。
f_1和 f_0 越接近,信号占用的带宽就越少,但两路信号之间的相互影响也随之增加。
误码性能分析:
P_e \approx \frac{1}{2}e^{-\frac{\gamma}{2}}
可将\gamma折算成\frac{E_0}{N_0},
\gamma =\frac{A^2}{2N_0B_{BPF}}=\frac{E_b}{N_0} \times \frac{R_b}{B_{BPF}}
\gamma与BPF的带宽密切相关,B_{BPF}越小,P_e也越小;
当B_{BPF}=R_b(最小理论值)时:
包络检波系统的误码率(误码率计算公式仅适用于解调器输入信噪比足够大的情况):
P_e \approx \frac{1}{2}e^{-\frac{E_0}{2N_0}}
2FSK的平均比特能量:
E_b= \frac{\int_0^{T_b}{(Acos2\pi f_1t)^2}\,dt+\int_0^{T_b}{(Acos2\pi f_0t)^2}\,dt}{2}=\frac{A^2T_b}{2}
例题:
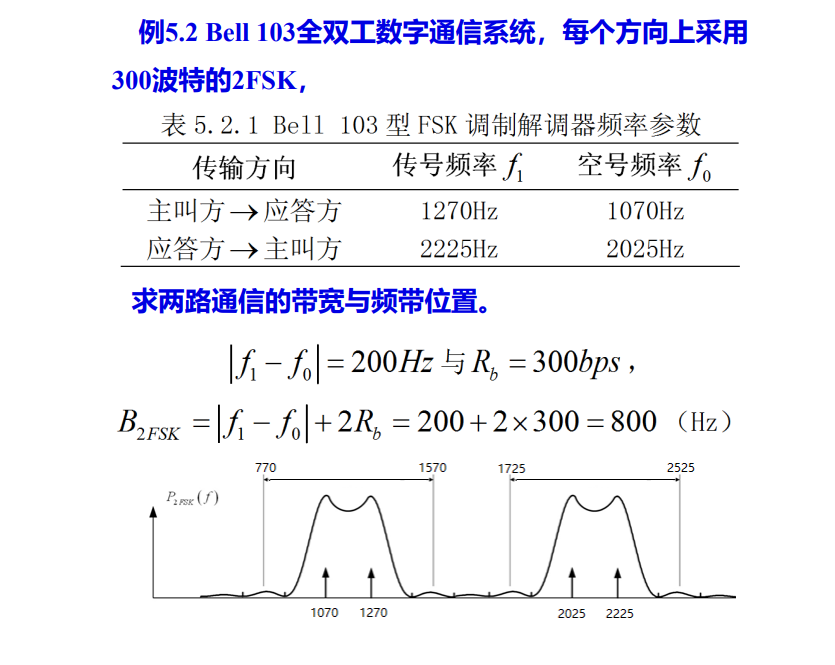
BPSK
概念:
2PAK或BPSK(二进制相移键控):利用两种相位来传输二元符号。
表达式:
其中,调制信号m(t) : 双极性二元NRZ基带信号
调制方法:
s_{2PSK}(t)=Am(t)cos2\pi f_ct,与2ASK的表达式相同,区别在于2ASK的m(t)是单极性信号,2PSK的m(t)是双极性信号。
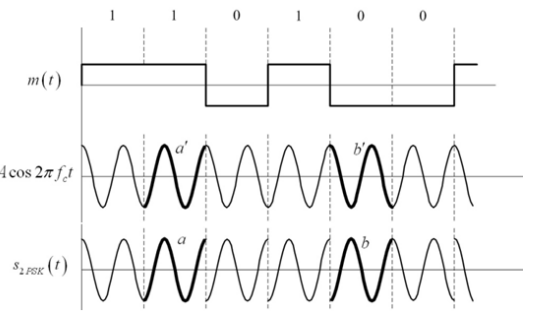
解调方法:
相干解调:
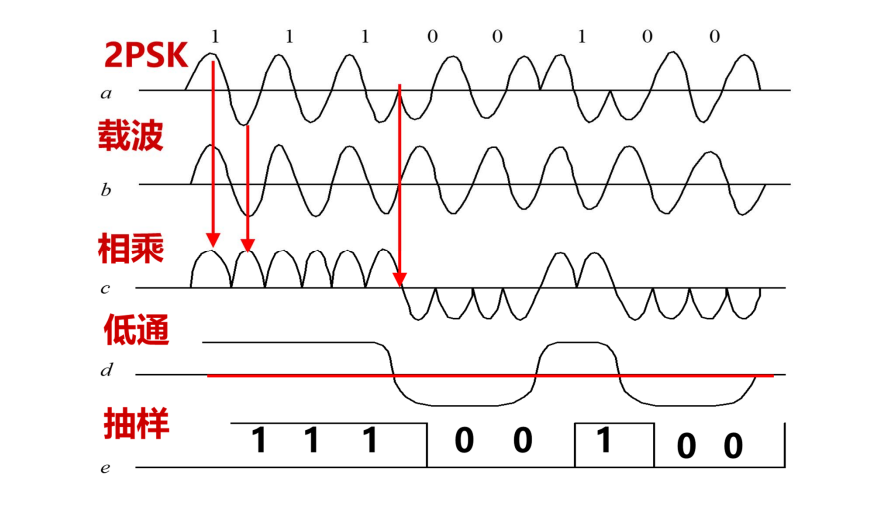
功率谱:
P_{2PSK}(f)=\frac{A^2T_b}{4}\{sinc^2[(f+f_c)T_b]+sinc^2[(f-f_c)T_b]\}
双极性基带信号m(t)的功率谱平移到±f,所以,形状与2ASK相同,但没有离散载波谱线。
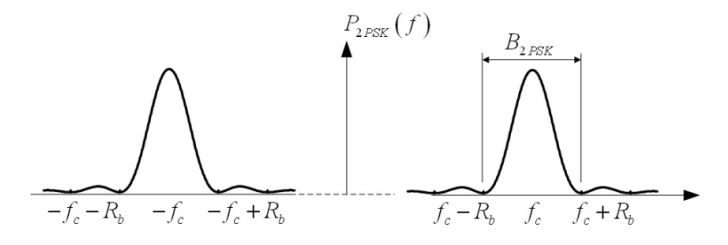
带宽:
基带信号m(t)带宽的2倍,B_{2PSK}=2R_b
如果基带信号m(t)是NRZ方波信号: B=1/T_b=R_b, 所以: B_{2PSK}=2R_b
理论上,二元基带信号最小带宽为R_b/2,因此2PSK最小带宽为B_{2PSK}=R_b
误码性能分析:
在使用MF(匹配滤波器)的时候:
P_b = Q(\sqrt{\frac{2E_b}{N_0}})
2PSK的平均比特能量:
E_b= \int_0^{T_b}{(Acos2\pi f_ct)^2}\,dt=\frac{A^2T_b}{2}
值得注意的是,2PSK的Pe与双极性NRZ基带传输系统的相同,2PSK的误码性能明显优于2ASK与2FSK,但这种系统需要进行载波同步,其复杂度要高出许多。
而当使用LPF(低通滤波器)的时候:
P_b = Q(\sqrt{\frac{A^2}{2N_0B_{LPF}}})= Q(\sqrt{\frac{E_b}{N_0}})
例题:

BDPSK(二进制差分相移键控)
概念:
为了解决解决不确定性反相问题,在2PSK基础上,分别在发送端与接收端增加差分编解码器,换言之,2DPSK = 2PSK + 差分编码

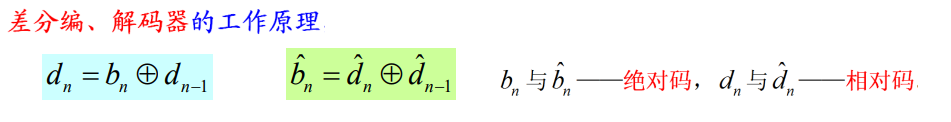
“相同为0,相异为1”,2DPSK通过相邻时隙载波相位的变化与否来“携带”信息
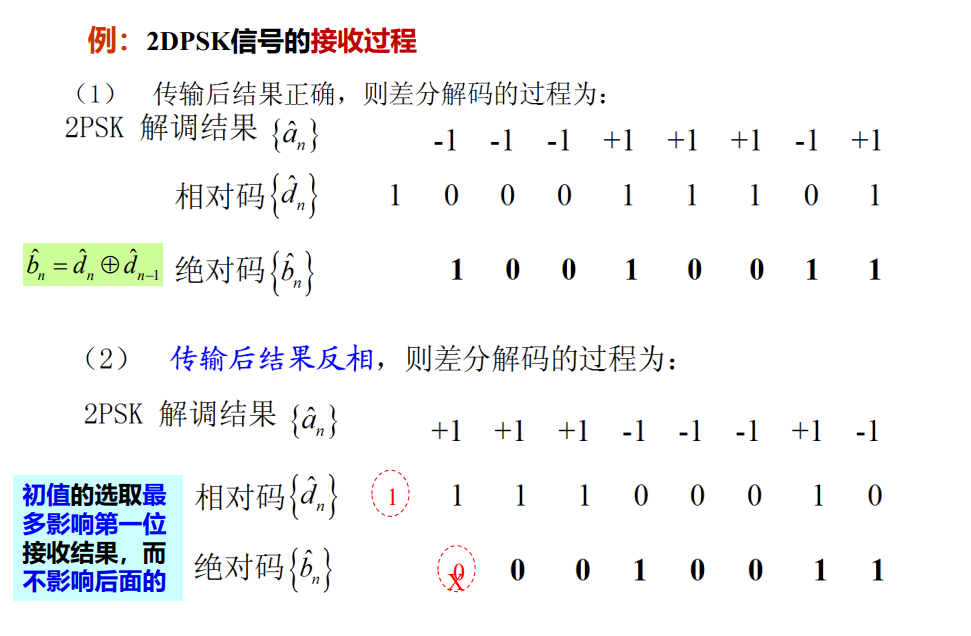
相干解调及其误码性能:
2DPSK的误码率接近2PSK的2倍:
P_{eDPSK}\approx 2P_{e2PSK}
2DPSK在使用MF(匹配滤波器)的时候:
P_e = 2Q(\sqrt{\frac{2E_b}{N_0}})
而当2DPSK使用LPF(低通滤波器)的时候:
P_b = 2Q(\sqrt{\frac{E_b}{N_0}})
差分检测及其误码性能:
比较两个相邻时隙上信号的相位,计算相位差,从而直接还原出绝对码(信息比特),特点是不需要本地振荡信号,属于是非相干解调
P_e \approx \frac{1}{2}e^{-\gamma}
可将\gamma折算成\frac{E_0}{N_0},
\gamma =\frac{A^2}{2N_0B_{BPF}}=\frac{E_b}{N_0} \times \frac{R_b}{B_{BPF}}=\frac{E_b}{N_0}
当B_{BPF}=R_b(最小理论值)时:
包络检波系统的误码率(误码率计算公式仅适用于解调器输入信噪比足够大的情况):
P_e \approx \frac{1}{2}e^{-\frac{E_0}{N_0}}
2DPSK的平均比特能量:
E_b= \int_0^{T_b}{(Acos2\pi f_ct)^2}\,dt=\frac{A^2T_b}{2}
注意:由于差分检测中乘法器的两个支路含有噪声,相乘后噪声增大,所以,差分检测的性能不如相干解调。
例题:

QPSK(四相移键控)
概念:
QPSK (Quadrature Phase Shift Keying)四相移键控,是一种多元(4元)数字频带调制方式,利用4种离散的相位状态传输四元符号序列,兼有采用四种相位和采用正交载波两种特性。
表达式:
s_{QPSK}(t)=Acos(2\pi f_ct+\theta_n),(n-1)T_s \leq t \leq nT_s
其中,\theta_n取值有四种可能,以传送的四元信号。
其中,比特对采用格雷码的好处是相邻相位对应的符号中只有1位不同,相位错误通常只导致1bit的损失。
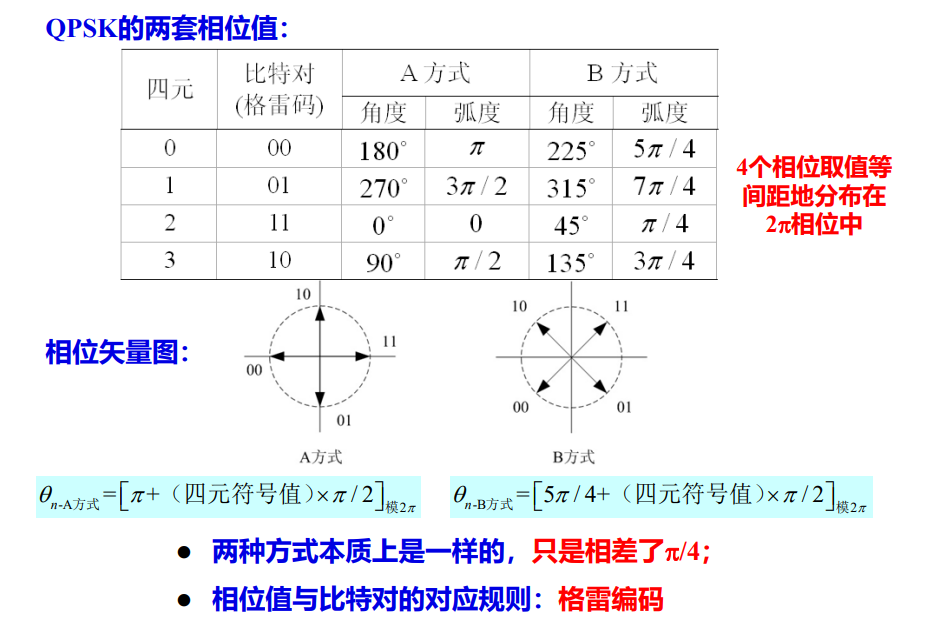
QPSK实质上是一种正交调制,它等于两路正交的2PSK叠加。
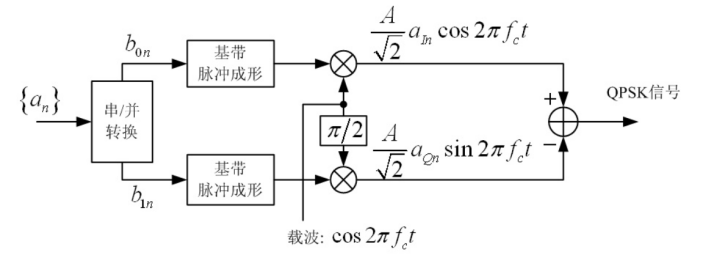
调制方法:
s_{DPSK}(t)=\frac{A}{\sqrt{2}}[a_{In}cos2\pi f_ct--a_{Qn}sin2\pi f_ct]
基本思想: 基于“QPSK等效于两路正交的2PSK之和”
调制器:
解调方法:
解调器:
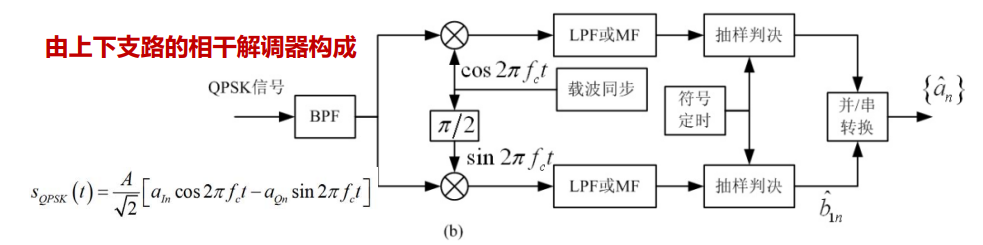
其中,同相与正交支路是彼此独立工作的
功率谱:
对于正交信号,信号的相关函数是它们相关函数之和,信号的功率谱是它们的功率谱之和,于是,由于两路正交2PSK信号的功率谱形状和载波位置都相同。
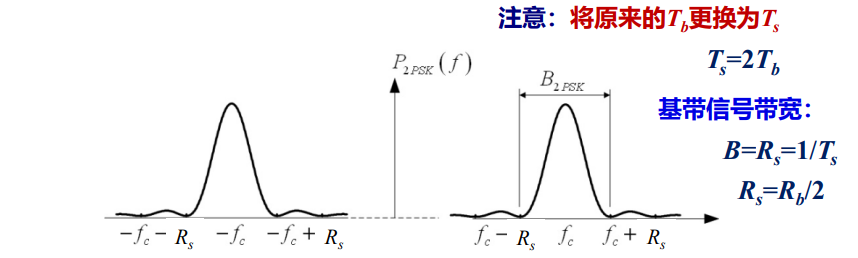
带宽:
QPSK信号的带宽:B_{QPSK}=2B=2R_s=R_b=\frac{1}{2}B_{2PSK}
QPSK每个时隙传输2比特,频带利用率是2PSK的两倍
误码性能分析:
QPSK系统与2PSK系统具有完全相同的误比特性能
P_b=P_{b-2PSK}
例题:
拿到一个二进制序列,先按照两个一组,转成格雷编码,再区别是采用A方式还是B方式进行载波相位序列的表示。

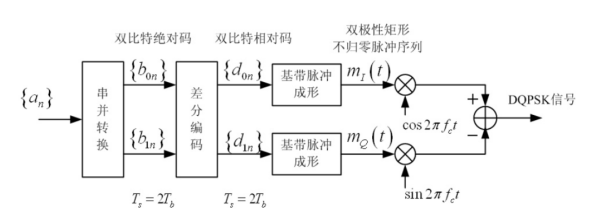
DQPSK(差分四相移键控)
概念:
QPSK信号的相干解调器也会出现“不确定性反相”现象,同样,解决这一问题的主要方法是使用DQPSK(差分四相移键控),也就是在QPSK基础上增加差分编、解码单元
调制方法:
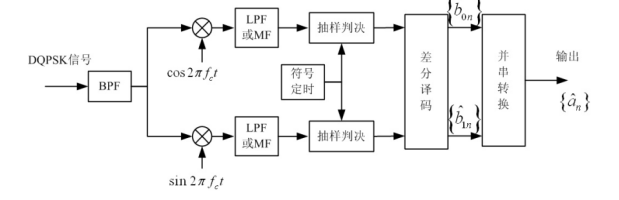
解调方法:
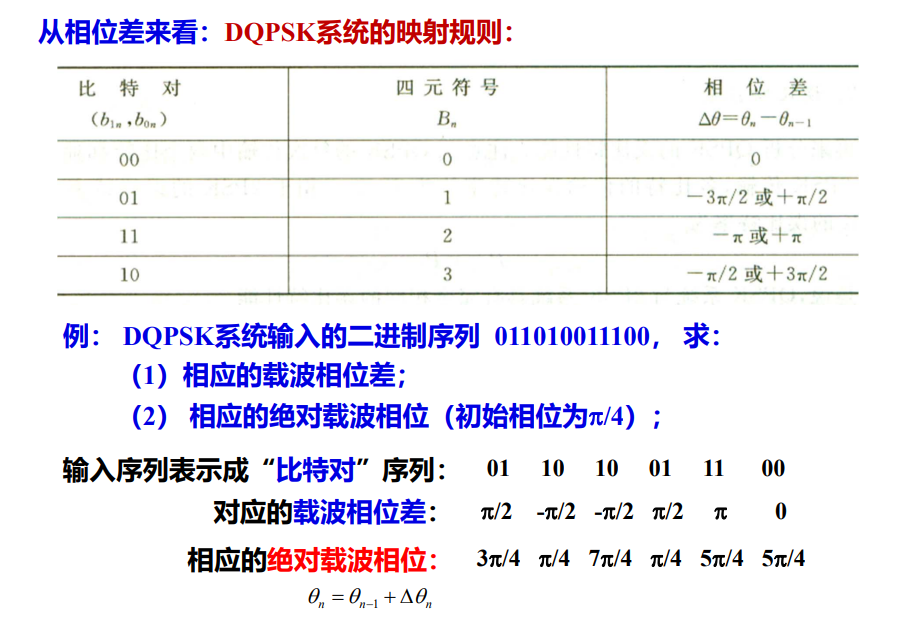
例题:
DQPSK并没有使用格雷编码,所以当我们拿到一个二进制输入序列的时候,不用把它转换成格雷码。而是直接两两分组进行映射。
QPSK的改进(OQPSK、\frac{\pi}{4}DQPSK)
OQPSK (偏移正交相移键控 Offset QPSK):
QPSK信号带外旁瓣高的原因——相位最大跳变为±\pi,减小相位跳变的有效方法:使两个正交支路的2PSK信号相互错开T_s/2的时间,使相位改变不同时发生
而OQPSK抗噪声性能,则与QPSK相同
\frac{\pi}{4}DQPSK:
调制方式交替地使用两套矢量图(相差\pi/4)产生波形;(当前时隙信号相位位于a图,下一时隙的相位必定位于b图,相对于上次点的相位变化为±\pi/4或±3\pi/4)
选取规则由下表决定:
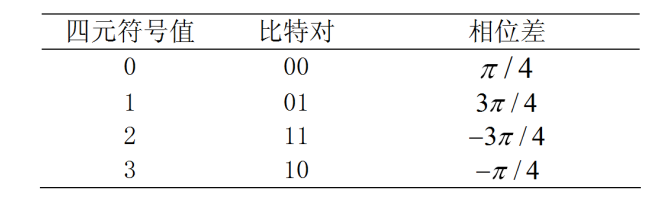
信号的最大相位变化为 ±3\pi/4;
调制时符号实际上对应于相邻时隙的相位差,调制解调框图与DQPSK基本一样——本质上是差分编码
相关解调时抗噪声性能也与DQPSK完全一样
例题:

基本频带调制的讨论
ASK与FSK相干解调
几种基本的频带调制信号的信号波形
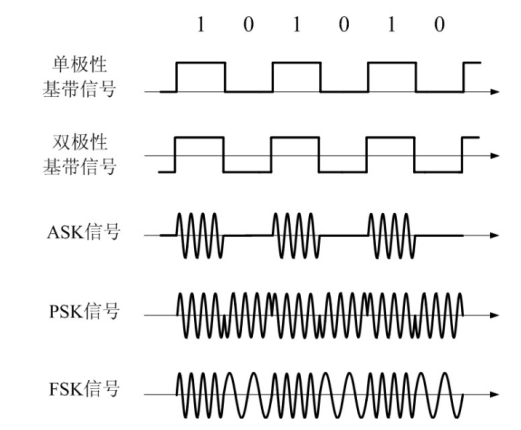
2ASK与2FSK在接收的时候,通常采用简单实用的非相干解调,但是也可以采用相干解调,所以,在题目中要求误码率的时候,如果没有特别说明,则需要一起求出非相干特调和相干特调的误码率。
| 2ASK | 2FSK | 2PSK | |
|---|---|---|---|
| 信号表达式 | Am(t)cos2\pi f_ct | Am(t)cos2\pi f_1t+A\overline{m(t)}cos2\pi f_2t | Am(t)cos2\pi f_ct |
| m(t) | 单极性信号 | 双极性信号 | 双极性信号 |
| 判决门限 | A/2 | 0 | 0 |
| 误码率(相干MF接收) | P_b = Q(\sqrt{\frac{E_b}{N_0}}) | P_b = Q(\sqrt{\frac{E_b}{N_0}}) | P_b = Q(\sqrt{\frac{2E_b}{N_0}}) |
| 平均码能量 | E_b=\frac{A^2T_b}{4} | E_b=\frac{A^2T_b}{2} | E_b=\frac{A^2T_b}{2} |
无ISI传输
频带信道、BPF、LPF等单元总是带宽有限的,所形成的等效基带信道也是带限的。为了实现可靠传输,频带传输系统中应该进行无ISI设计!
例题:

系统差错概率比较
几种基本的频带调制信号的误比特率公式:

几种基本的频带调制信号的误比特率图线:
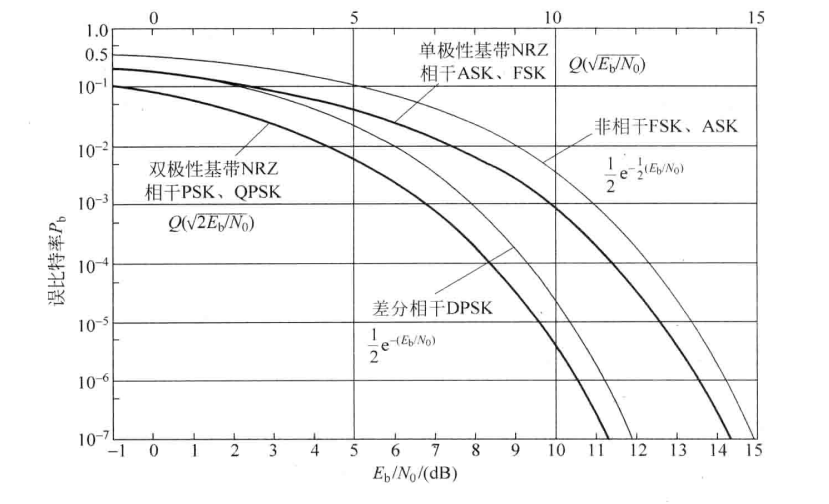
图像结论:
各条曲线都呈抛物线下降形状,靠左下方的曲线性能优良。

例题


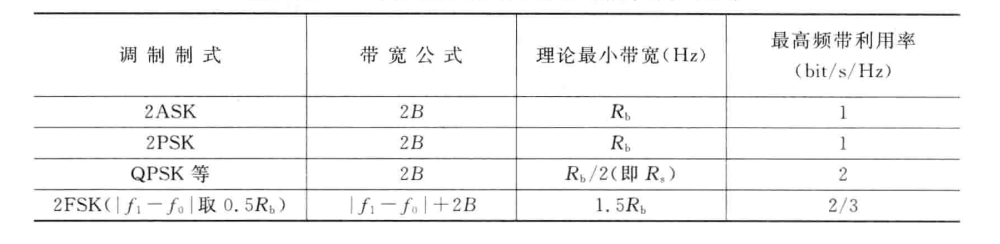
功率谱与带宽的讨论
几种基本的频带调制信号的带宽公式、理论最小带宽和最高频带利用率: