模拟信号数字化与PCM

模拟信号的抽样

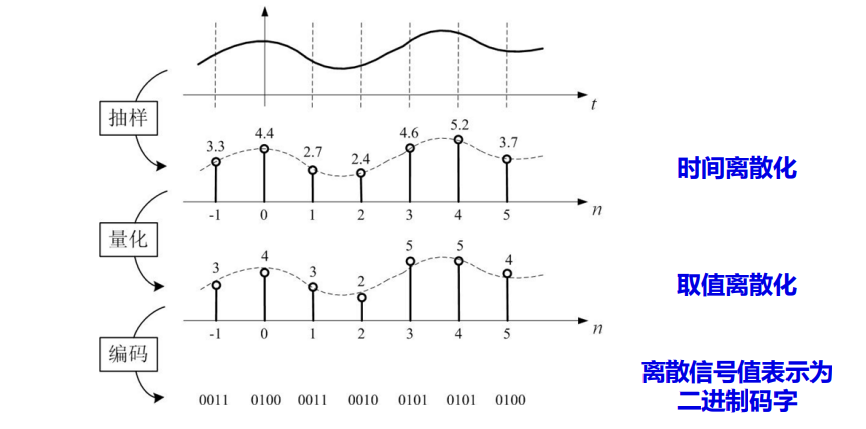
模拟信号的数字化是通信与信息处理的基础技术。语音、图像等许多消息信号必须转换成数字形式才能有效地进行存储、传输与处理。
把时间连续信号转换为时间离散序列通过抽样来完成。抽样过程应该完整﹑高效地保留原信号的信息﹐因此,要求得到的抽样序列能够完全还原出原来的模拟信号,并要求抽样序列的速率尽量的低。抽样定理是抽样的理论基础。
数字化过程：

带限(或低通)抽样定理

抽样或采样(sampling)就是在某些时刻上抽取信号值,形成反映原信号的样值序列。基本的抽样定理是针对带限或低通信号的，因此也称为带限(或低通)抽样定理，该定理可叙述如下:
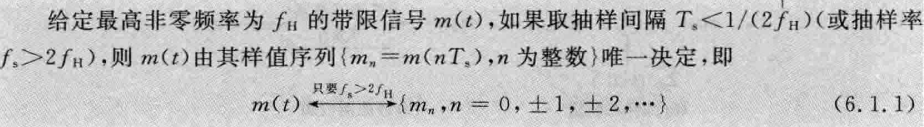
alt text
$f_H$ 是信号的带宽，在抽样定理中，抽样率必须大于 $2f_H$ ，所以 $2f_H$ 通常称为奈奎斯特频率（Nyquist frequency），对于低通或基带信号，其信号带宽 $f_H$ 正好为B，所以此时 $f_s >2B$

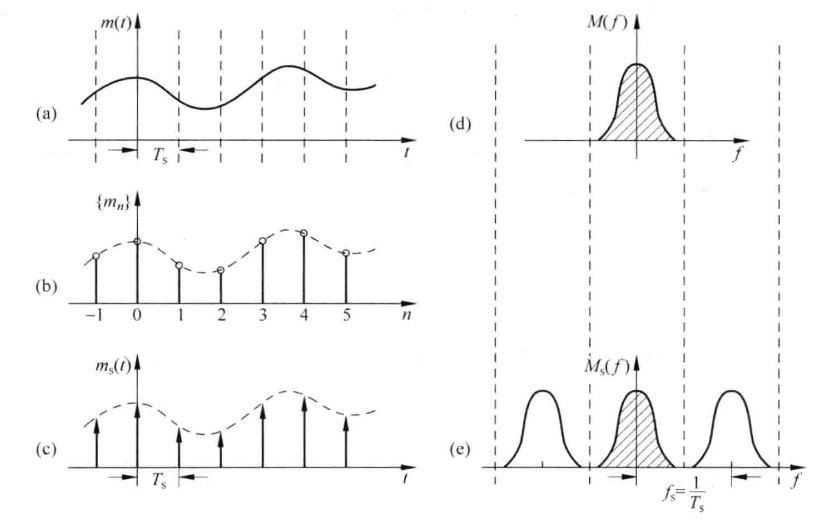
alt text
从时域上看: $m_s(t)=m(t)*\sum_{n} \delta(t-nT_s)=\sum_{n} m_n\delta(t-nT_s)$
从频域上看： $M_s(f)=M(f)*\frac{1}{T_s}\sum_{n} \delta(f-nf_s)=\frac{1}{T_s}\sum_{n} M(f-nf_s)$
结论：抽样的频域过程是频谱M(f)按 $f_s$ 进行周期重复；
条件 $f_s > 2f_H$ 保证了重复过程中频谱彼此不重叠，如果 $f_s < 2f_H$ 频谱会出现混叠现象。
还原 $M(f)$ 使用LPF： $m(t)=T_s* LPF[m_s(t)]$

带通抽样定理

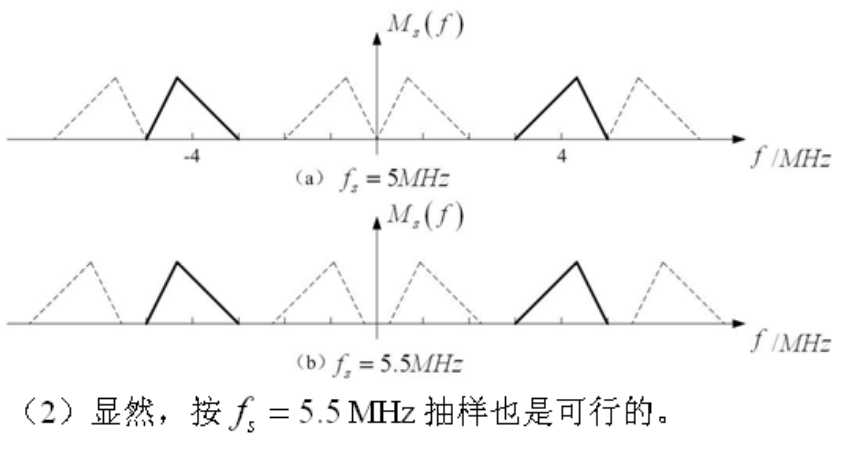
1. $f_H$ 是B的整数倍： $f_H=nB$
只要 $f_s$ 取2B，可以正确抽样。

2. $f_H$ 不是B的整数倍： $f_H=nB+kB，0<k<1$
取抽样率 $f_s=2B（1+k/n）=2f_H/n$ ，易见： $2B \leq f_S<4B$
还原 $M(f)$ 使用BPF对准频率范围： $f_L \leq |f| \leq f_H$ , $m(t)= BPF[m_s(t)]$

alt text

均匀量化与最佳量化

量化原理

量化（Quantization）是一个近似过程，以适度的误差为代价，使无限精度（或较高精度）的数值用较少的数位来表示，例如四舍五入量化。
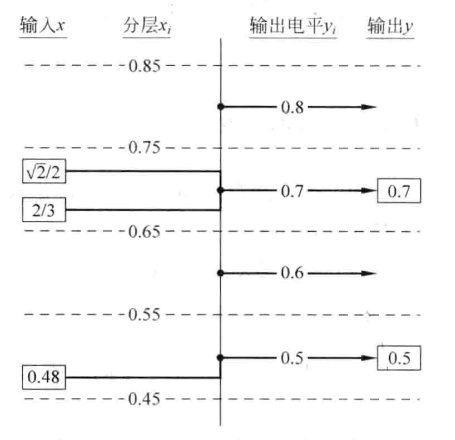
alt text
（1）输出电平：量化器将整个输入区域划分成多个区间，对落入每个区间的输入，以同一个 $y_i$ 值作为输出，一共M个；
（2）分层电平或阈值电平：各区间之间的分界 $x_i$ ，一共M+1个；
（3）量化电平数：所分区间的个数记为M；
（4）量化器的位数(或比特数)：实际上M常常取为2的幂次，不妨记为 $M=2^n$ ，n称为量化器的位数(或比特数)。
（5）量化误差（量化噪声）：由于量化器产生的误差，记为 $e_q=x-y=x—Q(x)$ ，采用均方误差(即噪声功率)来度量,即
$\sigma_q^2=E\{[x-Q(x)]^2\}=\int_{-\infty}^{\infty}[x-Q(x)]^2f(x)\,dx$
$f(x)$ ：输入x的概率密度
结论：好的量化器应具有较小的 $\sigma_q$ ：M越大，区间划分越细， $\sigma_q$ 越小。区间划分方法以及输出电平的选取都会影响 $\sigma_q^2$

均匀量化器(最基本的量化器)

M电平均匀量化器的结构特点：（输入范围为[-V，+V]）

均匀地划分出M个区间，各区间长度（量化间隔）相等
$\Delta=\frac{2V}{M}$
M+1个分层电平等间距排列
$x_i=-V+i\Delta ,\,\,\,\,i=0,1,2,3……,M$
M个输出电平位于各区间中心
$y_i=\frac{x_{i-1}+x_i}{2}=\frac{x_{i-1}+(x_{i-1}+\Delta)}{2}=x_{i-1}+\frac{\Delta}{2},\,\,\,\,i=0,1,2,3……,M$
量化误差（考虑输入x服从[-V，+V]）的均匀分布）：
$\sigma_q^2=\int_{-\infty}^{\infty}[x-Q(x)]^2f(x)\,dx=\int_{-V}^{V}[x-Q(x)]^2 \frac{1}{2V}\,dx=\frac{1}{2V}\sum_{i=1}^M \int_{x_{i-1}}^{x_i}[x-Q(x)]^2\,dx=\frac{\Delta^2}{12}$
即使输入不是均匀分布，当 M>>1 时,均匀量化器的均方误差仍为: $\sigma_q^2 \approx\frac{\Delta^2}{12}$

最佳量化器（使 $\sigma_q^2$ 达到最小的量化器）

因为 $\sigma_q^2$ 与输入信号特性及量化器的具体结构参数密切相关，所以要使 $\sigma_q^2$ 达到最小，最佳量化器必须针对输入来设计，最终结果也因输入特性的不同而不同。
Lloyd-Max （1960）规则：
给定输入信号特性 $f(x)$ 与量化电平数M时，最佳量化器结构参数满足:

\begin{cases} x_0=-\infty,x_M=+\infty\\ x_i=\frac{y_i+y_{i+1}}{2},i=0,1,2……，M\\ \end{cases}

$y_i$ 是个区间的质心， $x_i$ 位于相邻 $y_i$ 的中点：
$y_i=\frac{\int_{x_{i-1}}^{x_i}xf(x)dx}{\int_{x_{i-1}}^{x_i}f(x)dx}$

Lloyd-Max （1960）规则特点：
1.量化区间疏密不等，随 f(x)的高低分布；
2.取值概率大的地方区间划分细，取值概率小的地方区间划分粗；
3.各区间以其质心作为该区间的代表值——输出电平

显然，对于均匀分布而言，均匀量化器满足Lloyd-Max规则，是均匀分布的最佳量化器。

量化信噪比与对数量化

量化信噪比（度量量化器的性能指标）

量化误差的实际影响取决于它与信号的相对大小，因此，度量量化器性能的指标是量化信噪比，记为：
$(\frac{S}{N})_q=\frac{P_s}{\sigma_q^2}$
$P_s$ ：信号的功率
提高信噪比的措施：在量化器允许的输入范围——量化范围：[-V，+V]，使量化器工作在不过载的条件下，保持信号的幅度尽量大。

$M=2n$ 的均匀量化器信噪比:

\begin{cases} (\frac{S}{N})_q=\frac{P_s}{\sigma_q^2}=\frac{x_{rms}^2}{\sigma_q^2}=\frac{V^2}{\sigma_q^2} \times D^2\\ \\ \sigma_q^2 =\frac{\Delta^2}{12}=\frac{(\frac{2V}{M})^2}{12}=\frac{1}{3} \times 2^{-2n}V^2\\ \end{cases}

D：信号相对于量化范围的归一化有效值。
则：
$(\frac{S}{N})_q=3 \times 2^{2n}D^2$
分贝形式: $(\frac{S}{N})_q=4.77+6.02n+20log_{10}D(dB)$

alt text

特点：
（1）6dB规则：量化信噪比与位数n成正比，n每增或减1位，信噪比会变化约6dB
（2）受信号类型与幅度影响： $D_{max}$ 不一样
峰值信噪比：D=1时（理论是D的最大值）
$(\frac{S}{N})_{qPk_dB}=4.77+6.02n(dB)$
平均信噪比：均匀分布信号 $D_{max}=\frac{\sqrt{P_s}}{V}=\frac{\sqrt{3}}{3}$
$(\frac{S}{N})_{qAvr_dB}=4.77+6.02n-4.77=6.02n(dB)$

alt text

对数量化（非均匀量化）

模拟语音信号时一种峰平功率差异很大的信号，语音信号的有效幅度通常只有最大幅度的20%左右。均匀量化信噪比比峰值信噪比至少低十几个分贝！
电话语音信号的幅度难于控制：
（1）不同的发话人与情绪状态，平均功率变化范围达30dB左右；
（2）话机与数字化单元间的距离不同，衰耗差别可达2030dB左右
所以，在实际通信系统中：
面对约4050dB的动态范围，应提供至少25dB的量化信噪比。
alt text