通信原理学习——数字基带传输:
数字信息表现为离散序列的形式,数字通信系统的基本任务就是传输各种信息序列。但是实际上,所有的电子通信系统最终总是通过某种电气物理量来传递信息,例如电流与电压波形。这些物理量本质上都是时间连续的,因此,表征数字信息的离散序列必须变换为某种(时间)连续信号来传输。广义上来讲,这个将数字序列变换为一种(时间)连续信号的过程就是数字调制。
数字脉冲幅度调制(PAM)是一种基本、常用的数字调制方法﹐它利用脉冲幅度承载数字序列,从而构成连续信号。这类信号的功率谱密度通常从直流和低频开始,主要成分集中在零频率附近﹐因此是一种基带信号。PAM信号可以直接在合适的基带(低通型)信道中传输。
运用各种基带信号(通常采用正弦波来携带基带消息信号)传输数字序列的方法统称为数字基带传输( digital baseband transmission)技术,相应的传输信号与通信系统分别称为数字基带信号与数字基带传输系统。

数字信号及数字脉冲调幅信号:
基本特点:
(1)划分时隙,将时间依次划分为T长的时段
(2)将数据 a_n 逐个安排在各个时隙上(a_n是随机序列,所以,s(t)也是随机信号)
(3)利用不同幅度的脉冲来承载相应的数据

PAM信号特点:
(1)功率谱密度集中在零频附近,是基带信号
(2)可以在合适的基带(低通型)信道中传输
1.二元与多元数字基带信号
数据传输的基本概念:
(1)二进制序列(Binary sequence):两种取值。取值为 0、1(或+1、-1)
(2) 二元PAM信号(Binary PAM signal):两种电平,采用两种高度的脉冲。
(3) 定时 (Timing):用于接收信号时对准相应的脉冲,检测幅度。也称为同步信号。
(4)时隙 (Slot): 传输单个数据(0或1)的基本时间单元;序列的传输 —— “一个时隙一个数据位”
各种典型传输波形:
(1)单极性(Unipolar)与双极性(Polar)
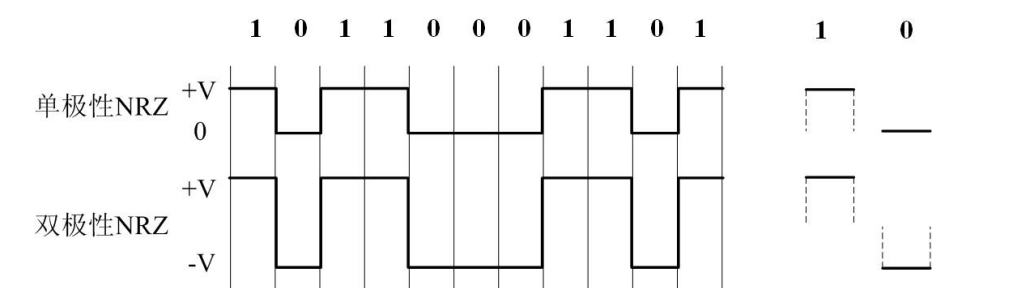
| 单极性 | 双极性 | |
|---|---|---|
| 说明 | 采用正电平和零电平,因而只用一种极性 | 采用正、负电平,有两种极性 |
| 优点 | 可以使用单电源电路,简单。 | 没有直流分量,传输线路无须具有直流耦合能力;抗噪能力强,传输距离远 |
| 缺点 | 波形中具有直流分量,只能在直流耦合的线路中使用 | 产生电路较为复杂,既需要正电源,又需要负电源 |
(2)归零(RZ)与非归零(NRZ)

| 非归零(NRZ) | 归零(RZ) | |
|---|---|---|
| 说明 | 每个脉冲的电平在整个Ts内保持不变(中途不回归零电平 | 每个脉冲的电平在一个时隙的中途回归零电平,脉冲的宽度通常是时隙的1/2 |
(3)差分码和相对码
不用电平的绝对值而用电平的相对变化来表示符号的0和1。
符号“1”——电平发生相对翻转
符号“0”——波形保持不变

这个相对陌生一点,那如何去读?上升沿和下降沿读作“1”,并且上升沿和下降沿所在的那个T不用读了;上横线和下横线读作“0”,over
【说明】
- 不同的脉冲波形具有不同的频谱特性,而这些特性使得它们分别适合于不同的场合;
- 二元序列是最基础与通用的信息序列形式;
- 数字通信的两个基本问题:1.传输数率 2.功率谱和占用的带宽。
数字基带信号的传输速率
符号速率(Symbol rate)(码元速率、波特率):R_s,单位时间传送符号的数目
R_s=1/T_s \,\,\,\,symbol/s (或者 baud)\\T_s:符号间隔
比特率(Bit rate):R_b,每秒传送的比特数目(单位:bps)
R_b=1/T_b \,\,\,\,bps\\T_s=KT_b\,\,\,\,T_b:比特宽度
两者之间的关系:
R_b=KR_s=R_slog_2M
符号速率R_s——考虑的是数字基带信号以符号为基本传输单位;
比特率R_b——以比特为通用单位,是数字通信系统统一的速率单位.
【例】二元序列{101101000111101011},传输时间为1ms
求:1. 相应的四元与八元序列;
2. 相应的 Rb,Rs,与 Ts
解:
| M | 序列长度 | T_S(ms) | T_b(ms) | R_s(baud) | R_b(bps) |
|---|---|---|---|---|---|
| 二 | 18 | 1/18 | 1/18 | 18000 | 18000 |
| 四 | 9 | 1/9 | 1/18 | 9000 | 18000 |
| 八 | 6 | 1/6 | 1/18 | 6000 | 18000 |
可以得到以下结论:
当一串m元序列转变为相应的n元序列后,各自对应的T_b(ms)和R_b(bps)都保持不变;序列变短以后,T_S(ms)会相应地变大(T_S(ms)=1/序列长度),R_s(baud)相应变小。
2.数字信号的功率谱与带宽
信号的功率谱
对于给定的数字PAM信号:
数字PAM信号的功率谱与两个因素有关:
- 数字序列{a_n}的自相关函数 R_a(k);
- 脉冲g_T(t)的频谱特性 G_T(f)
假设:信息序列均值:m_a=E[a_n] ,方差:\sigma^2_a=E[a^2]-m^2_a
那么,相应的MPAM信号的功率谱密度为:
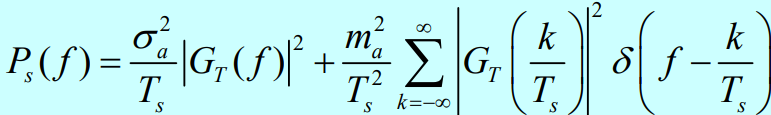
前面部分是连续谱,由脉冲g_T(t)的能量谱决定,后面部分是离散谱,线谱的功率正比于脉冲能量谱在该处的值。所以,我们会得到:PAM信号的功率谱与它的元数M无关!2PAM与MPAM功率谱相同!
特别地,当 {a_n} 的均值 m_a=0 时,离散线谱消失:
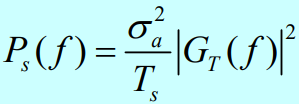
【例】求采用NRZ脉冲的MPAM信号功率谱:

解:根据图像确定g_T(t)以后,我们可以求出G_T(f):

将其带入到之前的P_s(f)的表达式中:
k为非0整数时,sinc2(k)=0,此时功率谱中只含有离散的直流线谱:
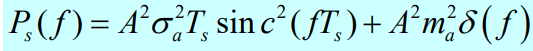
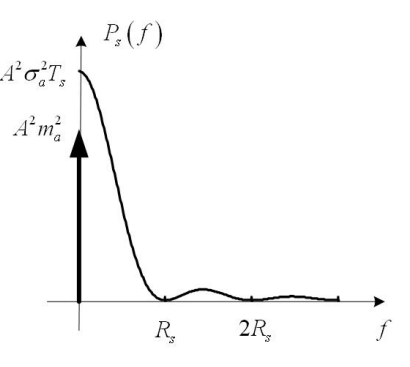
特别地,2PAM信号(两种情形):T_s=T_b
第一种,双极性信号:m_a=0,\sigma^2_a=1;
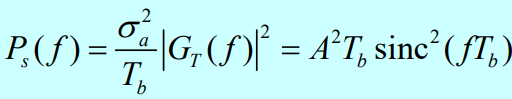
第二种,单极性信号:m_a=1/2,\sigma^2_a=1/4;
此时,双极性与单极性的核心差别在于是否有直流成分
信号的带宽
从功率谱分析看出,矩形MPAM信号:
1.绝对带宽无穷大;
2.信号的主要功率集中在零频附近。
矩形MPAM信号的第一零点带宽:B_T=R_s=1/T_s=R_b/K
显然有符号速率R_s可以方便地计算信号的带宽(Hz)
| 符号率 | 带宽 | |
|---|---|---|
| 2PAM | R_b | B_T=R_b |
| MPAM | R_b/K | B_T=R_b/K |
当M越高时,所需带宽越小,但是抗噪性能降低,接收复杂。
【例】采用二元、四元与八元PAM按照18kbps传输信息序列,如果脉冲为双极性NRZ码,试求相应信号的带宽。
解:比特率 都为R_b=18 kbps
符号速率 R_s= R_b/K ,所以分别为:18kbaud,9kbaud,6kbaud
相应的第一零点带宽分别为:18kHz,9kHz,6kHz
3.二元信号的接收方法与误码分析
噪声中二元信号的接收方法
在噪声环境中接收信号的关键是尽量抑制噪声,于是出现来两种方式:第一种是低通滤波,第二种是匹配滤波
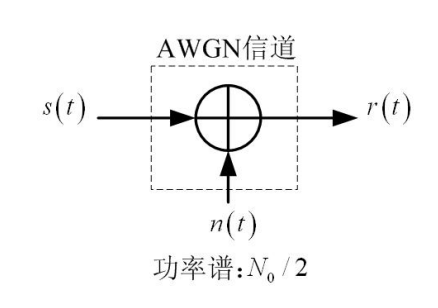
其中,两者的流程三个步骤:滤波——采样——判决,匹配滤波器详细说明:匹配滤波器
低通滤波方便理解一点,在这里进行简单说明,
滤波过程:对于LPF的带宽:既要足够宽,保证信号尽量完整通过;又要相当窄,最大限度地滤除噪声。对于2PAM矩形NRZ信号,理论上可以取B=R_s,实际中通常取:B \geq 2R_s
采样过程:使用定时信号进行采样
判决过程:对于最佳判决门限:取在两种脉冲电平的中间双极性NRZ:V_T = 0,单极性信号:V_T = A/2
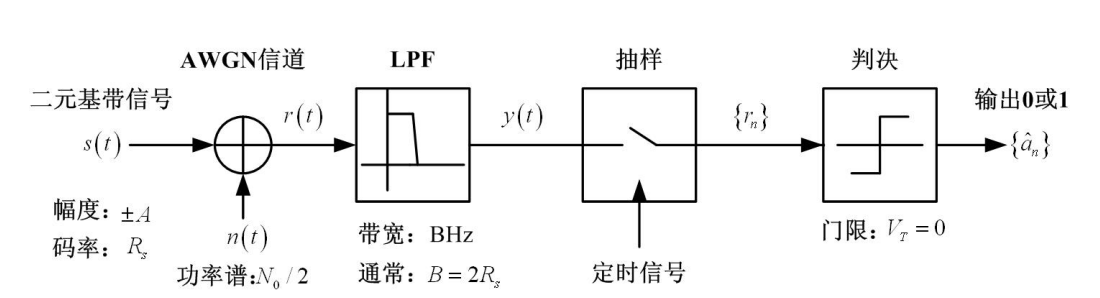
对比低通滤波和匹配滤波而言,两者具有完全相同的结构:前端都设置有一个抑制噪声的接收滤波器h(t),不同之处在于:h(t)不一样,导致了具有不同的性能
接收系统的误码性能
数字基带传输的具体抗噪性能采用误码率或误比特率衡量。
(1)误码率或误符号率(symbol error rate): 传输各个码元或符号发生错误的概率
P_e \approx \frac{错误码元数目}{总传输的码元数目}
(2)误比特率:传输各个比特发生错误的概率
P_b \approx \frac{错误比特数目}{总传输的比特数目}
对于二元通信系统:P_e=P_b
对于多元通信系统:P_e \geq P_b
误码过程的分析
影响到系统误码性能的几个因素:1.噪声;2.最佳接收;3.判决门限的设置
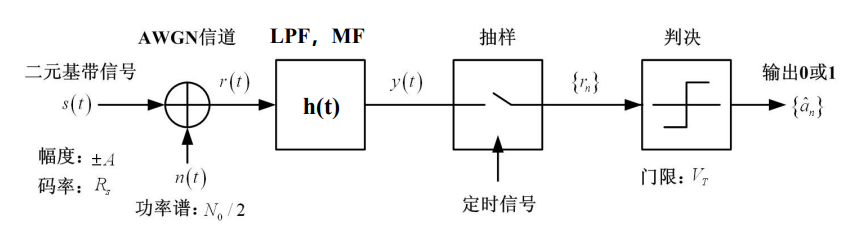
1.噪声造成抽样值的随机性
当发送0的时候:
基带传输信号:s(t)=A_0g_T(t)
接收信号:r(t)=A_0g_T(t)+n(t)
经过滤波器后的信号:y(t)=A_0g_T(t)*h(t)+n(t)*h(t)=y_{s0}(t)+y_n(t)
抽样值:r=y_{s0}+y_n,且 r\sim N(y_{s0},\sigma_n^2)
所以概率分布满足高斯分布:
同理在发送1的时候也有相同情况:
所以概率分布同样满足高斯分布:
因为噪声的影响,抽样值r是高斯随机变量,其均值因发送码元不同而不同,但方差都一样。
2.判决规则与错判概率
在抽样判决的环节通常由抽样值r判断发送的码元是0或者1,抽样值r如果小于V_T就会判决此时的结果是0,反之,如果抽样值r如果大于V_T就会判决此时结果为1。但是由于r是随机的,判决有可能出现错误。
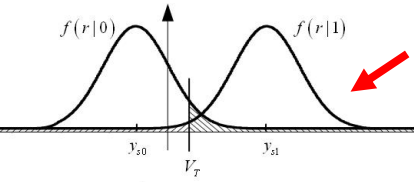
那么此时判决出错的概率可以表示为:
P(error|a_n=0)=P(r \geq V_T| a_n=0)= \int_{V_T}^\infty f(r|0)\,dr
P(error|a_n=1)=P(r < V_T| a_n=1)= \int_{-\infty}^{V_T} f(r|1)\,dr
总的平均误码率:
P_e=P(a_n=0)\int_{V_T}^\infty f(r|0)\,dr +P(a_n=1)\int_{-\infty}^{V_T} f(r|1)\,dr
3.最佳门限与最小平均误码率
由上述公式可得门限表达式:
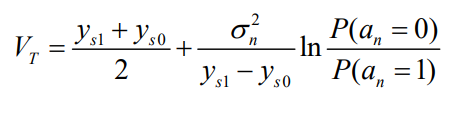
经分析,当发送符号先验等概时,即P(a_n=0)=P(a_n=1)=1/2时有最佳门限:
V_T=\frac{y_{s1}+y_{s0}}{2}
此时有最小平均误码率:
说明:该结论具有一般性;适用于不同信号模式与不同接收系统,其中y_{s1}、y_{s0}对应于信号的强度,由信号电平与接收滤波器共同决定;\sigma_n对应于噪声的影响,由接收系统决定。
常用函数:这个函数会在后面经常出现
Q(X)=\frac{1}{\sqrt{2\pi}}\int_{x}^\infty e^{ -\frac{z^2}{2}} \,dz

所以通过计算可以得到主要2PAM数字基带传输系统的P_e(P_b)(假设二元信息序列取值等概P(a_n=0)=P(a_n=1)):
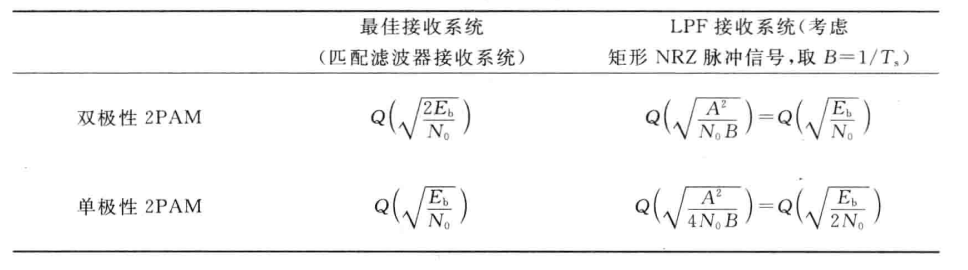
由上图可以得出基本结论:
1.双极性信号比单极性信号抗噪性能好
2.匹配滤波器比低通滤波器接接收性能好
3.最佳基带传输系统是双极性信号 + 匹配滤波器
【例】计算E_b/N_0对误比特率P_b的影响,分别考虑单极性与双极性信号的匹配滤波器系统,给出P_b达到10^{-2}、10^{-4}····10^{-12}所要求的E_b/N_0,并估计按R_b=1Mbps进行二元传输的平均错误间隔。
解:假设总传输时间为1s,
所以总传输的比特数目为R_b*T=1Mbps*1s=1Mbit,错误比特数目为P_b*总传输的比特数目=10^{-2}*1Mbit=10^4bit,
所以平均错误间隔为T/错误比特数目=1s/10^4bit=10^{-4}s,其余以此类推。
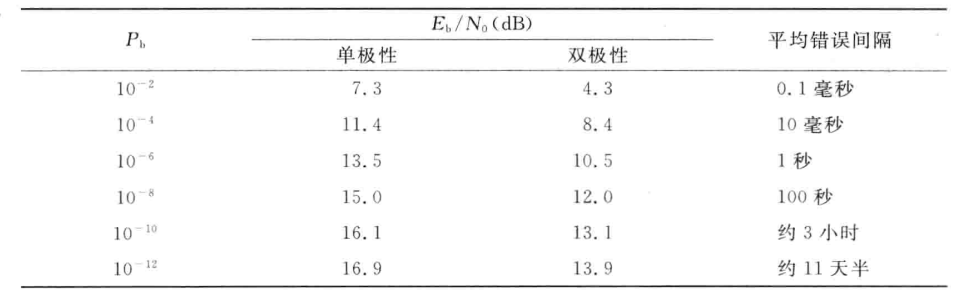
4.码间串扰(inter-symbol interference,ISI)与Nyquist准则
由于传输后的脉冲存在前导与拖尾,它在完成传递a_n的同时也不同程度地干扰了前后码元的接收。
影响基带传输系统的不良因素包括噪声和ISI,消除噪声前面介绍了主要采用LPF或MF来抑制;
对于消除ISI允许h(t)有 “拖尾”,但是要求:在t_0+T_s,t_0+2T_s等后面码元抽样判决时刻上正好为0,也就是所谓“串而不扰”,这也是无ISI的真正含义。
定理(Nyquist准则):要保证接收时无ISI,必须满足
1.从时域来描述,传输系统总的冲激响应:h(t)=g_T(t)*c(t)*g_R(t)
(可以通过控制发送滤波器g_T(t)与接收滤波器g_R(t)来实现)
2.从频域来描述,传输系统总的传递函数:
这表示是H(f)按 1/Ts周期重复的结果
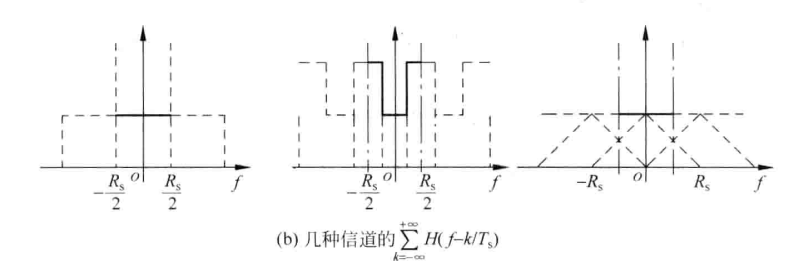
【例】几种传输特性H(f),传输率R_s,是否存在ISI?
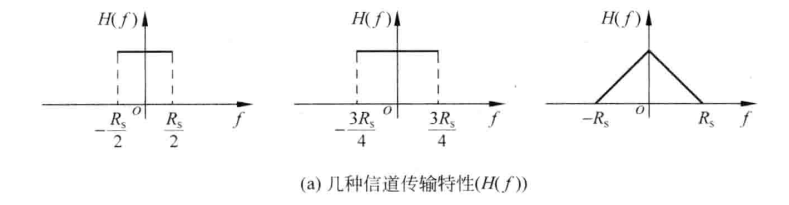
解:在第1、3信道上无ISI,而在第2信道上有ISI。
带限信道上的无码间串扰传输
假定 H(f) 的带宽为WHz,系统以数据速率R_s=1/T_s传输数字序列
1.如果带宽W<R_s/2=1/2T_s,也就是:R_s>2W时,图像如下:
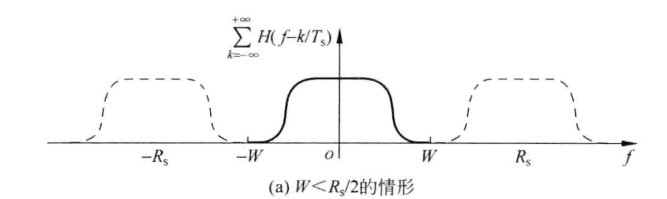
结论:此时并不满足\sum_{k={-\infty}}^{+\infty} H(f-\frac{k}{T_s})=常数,所以带宽太窄,一定存在ISI
2.如果带宽W=R_s/2=1/2T_s,也就是:R_s=2W时,图像如下:
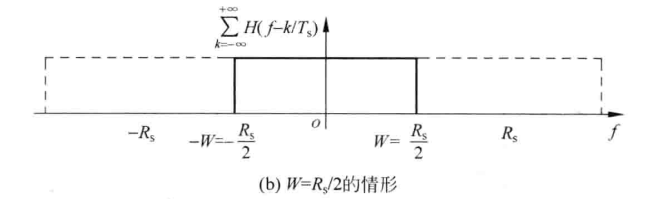
结论:当且仅当 H(f)正好为带宽是R_s/2Hz的理想LPF时,一定无ISI
3.如果带宽W>R_s/2=1/2T_s,也就是:R_s>2W时,图像如下:
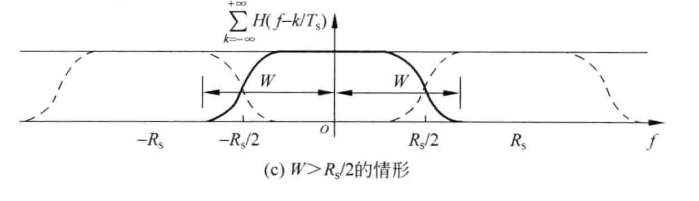
结论:存在某些合适的 H(f)可以满足无ISI
同时综上,我们可以得到一些重要结论:
(1)在无ISI的要求下,W Hz宽的基带信道每秒最多只能传输2W个符号;如果符号是M元的,最大比特传输率为 R_b = 2Wlog2M bps;2W波特——基带传输系统的奈奎斯特速率
(2)频带利用率 —— 单位带宽的传输速率
\eta=\frac{传输速率}{占用频带宽度}=\frac{R_s}{B_T}(baud/Hz)=\frac{R_b}{B_T}(bps/Hz)
在无ISI传输中,一定有
\eta \leq 2 baud/Hz, \,\,\,或者\,\,\, \eta \leq 2log_2M bps/Hz
所以,二元传输方式\eta的上限为 2bps/Hz,提高\eta的基本途径就是增加信号的元数M
升余弦滚降滤波器(RC)
升余弦滚降(RC)滤波器频谱:
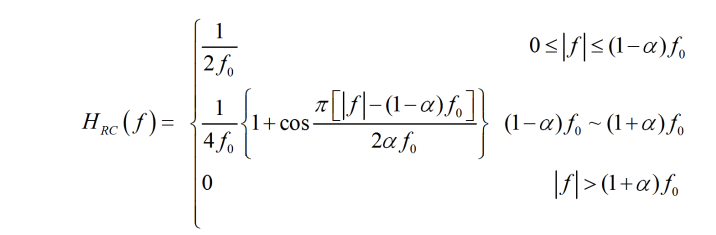
其中,滚降因子:0 \leq \alpha \leq 1,在实际当中通常\alpha取0.3;f_0=6dB带宽
最大带宽(绝对带宽):W=(1+\alpha)f_0
解题基本思路:

【例】某基带传输系统信道的频响特性在5MHz内平坦。试求:(1)无ISI的最大传输码率;(2)采用\alpha=0.3的RC时的最大传输码率;(3)采用\alpha=0.3的RC时如何实现R_b=10Mbps传输
解:(1)W=5MHz,当\alpha=0时,R_s(max)=2W baud=10 Mbaud
(2)由于W=(1+\alpha)f_0,f_0=R_s/2,则
R_s=\frac{2W}{1+\alpha}=\frac{10M}{1.3}=7.69 Mbaud
(3)在(2)中我们已经求解过采用\alpha=0.3的RC时的最大传输码率为7.69(Mbaud),由于(3)题目中要求R_b=10Mbps,那么如果采用二元传输,则R_s=10(Mbaud)>7.69(Mbaud),因此,无法进行无ISI传输。如果改用四元传输,R_s=5(Mbaud)<7.69(Mbaud),此时可以满足条件。



