通信原理学习——匹配滤波器
出现的原因:
在数字通信系统中,如何从含有加性噪音的接收信号x(t)中准确判断出是否已经接收到s(t),是一个基本问题。换句话说,通信系统的质量取决于接收系统的性能。
从接收系统的角度来看,这涉及到最佳接收或信号接收最佳化问题。
“最好”或“最佳”不是绝对的,而是在某个约束条件下的一个相对概念。在数字通信系统中,常用的最佳准则是最大输出SNR和差错概率最小准则。
因此,一种LTI滤波器,即匹配滤波器出现来帮助我们处理x(t),希望处理后的输出信号y (t)最有利于判断s (t)收到与否。它能够从噪声当中将信号提取起来,并在t=t_0时刻提供最佳判断依据,因为此时信号最大限度地超过了背景噪声。
原理:
匹配滤波器:在加性白噪声背景下,对某一具体信号能获得最大输出信噪比的线性滤波器。
基本流程如下:匹配滤波器主要包括三步:滤波——抽样——判决
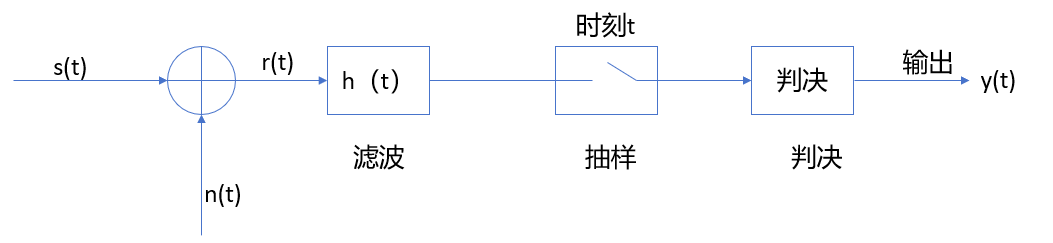
抽样判决器输出数据正确与否,与滤波器输出信号波形和发送信号波形之间的相似程度无关,而只取决于抽样时刻信号的瞬时功率与噪声平均功率之比,即信噪比。
信噪比越大,错误判决概率(Pe或者Pb来衡量)就越小;
信噪比越小,错误判决概率(Pe或者Pb来衡量)就越大。
为了使误码率Pe尽可能小,就要选择滤波器传输特性使滤波器输出SNR尽可能大的滤波器。当选择的滤波器传输特性使输出SNR达到最大值时,该滤波器就称为输出SNR最大的最佳线性滤波器。
那什么样的滤波器的传输特性能够使SNR达到最大值呢?
匹配滤波器的单位冲激响应为h(t)=cs(t_0-t),
式中,c与t_0为任意非零常数。在r(t)=s(t)+n(t)输入下,h(t)使使输出信噪比在t_0时刻最大的滤波器。
下图是s(t)和h(t)的图像对比:

对于因果系统, 匹配滤波器的单位冲激响应,h(t)应满足下列式子:
h(t) =
\begin{cases}
cs(t_0-t), t\geq0\\
\\
0, t<0\\
\end{cases}
要满足上式条件, 必须有:s(t_0-t), t<0成立,即s(t)=0,t>t_0
若输入信号在T时刻结束,则对物理可实现的匹配滤波器, 其输出最大信噪比时刻t_0必须在输入信号结束之后,即t_0 \geq T。对于接收机来说,t_0是时间延迟,通常总是希望时间延迟尽可能小,因此一般情况可取t_0=T
若输入为s(t), 则匹配滤波器的输出信号为:
s_0(t)=s(t)*h(t)=cR(t-t_0)
其中, R(t)为输入信号s(t)的自相关函数。这表明:
1.匹配滤波器输出=输入信号的自相关函数的c倍。通常取c=1。
2.其在t0时刻得到最大输出信噪比:
r_{omax}=\frac{2E}{n_0}
说明
对前文中给出的匹配滤波器的定义(在加性白噪声背景下,对某一具体信号能获得最大输出信噪比的线性滤波器)作出下列说明:
1、背景是白噪声,输出信噪比是其输出端信号瞬时(不是“平均”)功率与噪声平均功率之比。
2、滤波器限于线性:可以是放大器、混频器、相干乘积型检波器等,不能表述限幅器、包络检波器等
3、最大信噪比可等价于最小错误概率。
4、要求输入信号是时限信号(0,T)。物理意义:匹配滤波器的输出信噪比与输入信号能量成正比;若输入信号尚未结束,就无从得到输入信号的全部能量;另一方面,一旦输入信号结束,全部能量皆被利用,从而输出信噪比达到最大。常常取t_0=T
5、匹配滤波器是一个线性滤波器,但是它并不保持输入信号的形状。相反,它会使输入信号波形失真,以此来获得最大输出信噪比。
6、匹配滤波器频率特性正比于输入信号频谱的共轭(除固定延迟t_0外)
举例
【例1】设输入信号如图(a),试求该信号的匹配滤波器传输函数和输出信号波形。
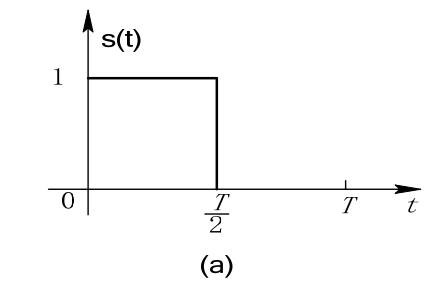
解:输入信号s(t):
所以,匹配滤波器传输函数h(t):
取c=1,t_0=T,则
h(t)=s(T-t)
图像如下:

所以,输出信号波形s_0(t):
s_0(t)=R(t-t_0)=\int_{-\infty}^{+\infty} s(x)s(x+t-t_0)\,dx
过程如下:

【例2】已知匹配滤波器的单位冲激响应h(t)如图所示。试求:
(1)输入信号波形;
(2)匹配滤波器的输出波形;
(3)最大输出信噪比时刻和最大输出信噪比;
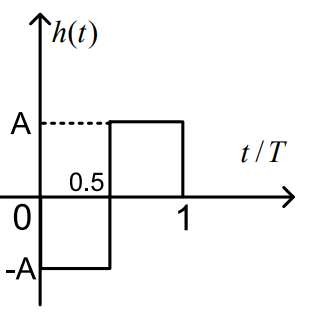
解:根据图像写出h(t)函数:
(1) 根据匹配滤波器原理,输入信号:
图像如下:
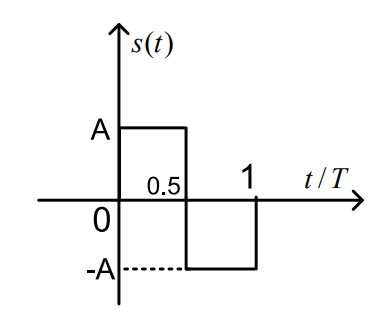
(2)根据匹配滤波器原理,匹配滤波器输出为:
图像如下:
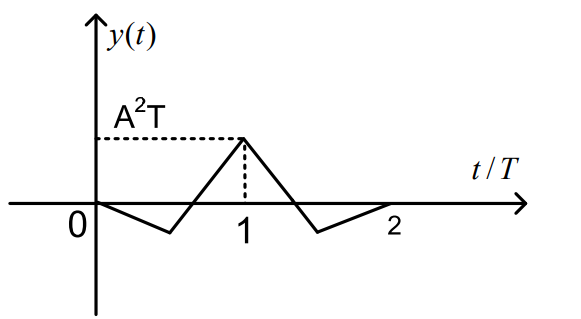
(3)最大输出信噪比出现时刻应在信号结束之后,即t_0=T;最大输出信噪比为:
r_{omax}=\frac{2E}{n_0}=\frac{2A^2T}{n_0}



