信道均衡实验
一、 实验目的
1、了解均衡技术的原理;
2、了解信道均衡的作用以及分类;
3、掌握迫零均衡算法;
4、了解最小二乘算法。
二、 实验原理
1、均衡原理
在数字通信系统中,由于多径效应、信道带限等因素的影响,在接收端会形成码元(符号)拖尾,拖尾部分与相邻码元(符号)叠加,产生符号间干扰或码间干扰(ISI)。为了消除干扰,在基带系统中插入一种滤波器,来补偿整个系统的幅频和相频特性,从而使包含该滤波器的传输系统的特性满足无码间串扰的条件。
这个对系统校正的过程称为均衡,实现均衡的滤波器称为均衡器。使用均衡器后的通信系统的简化框图如图 2-1 所示。
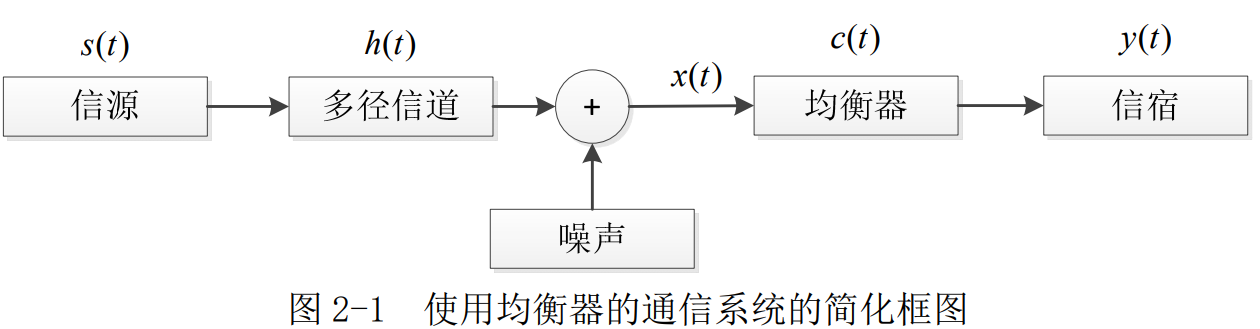
图 2-1 中,该通信系统在接收机的基带处理部分加入了自适应均衡器。图中s(t)为基带传输信号,h(t)为信号经过多径信道后的冲激响应,加入基带噪声后,根据最佳检测理论,接收机设计使等效传输信道符合最大输出信噪比准则,此时均衡器接收端的信号为:
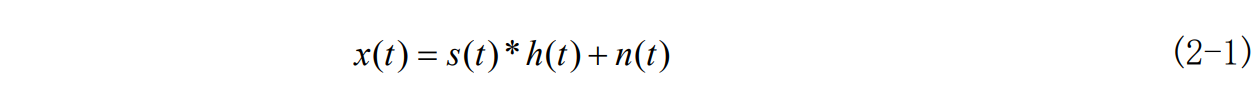
则均衡器的输出为:
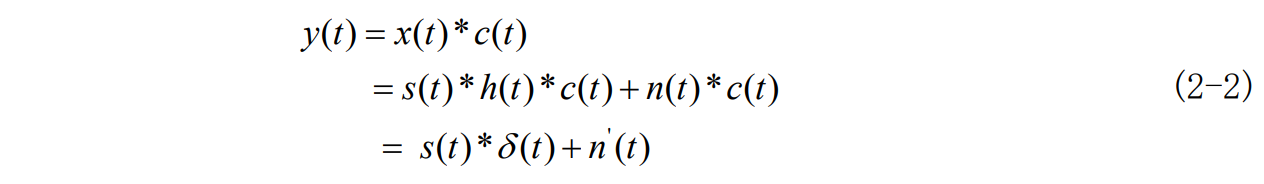
均衡器分为时域均衡器和频域均衡器。时域均衡又分为线性均衡和非线性均衡两类。其中线性均衡器可以用横向滤波器和网格滤波器来实现,本次实验仅考虑横向滤波器。
2、横向滤波器
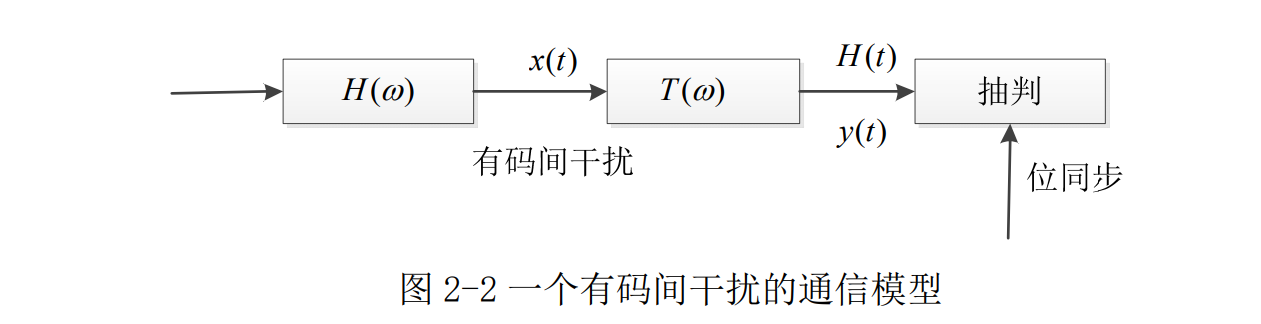
图 2-2 是一个有码间干扰的通信模型,当H(w)不满足无码间干扰条件时,输出信号x(t) 存在码间干扰,为此,在H(w)之后插入一个横向滤波器T(w),形成新的总传输函数H'(w),且H'(w)=H(w)T(w),故只要H'(w)满足式 2-3 和2-4
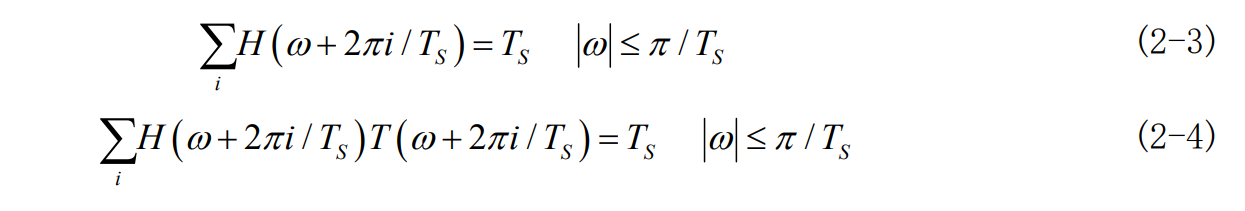
如果T(w)是以2\pi i/T_s为周期的周期函数,那么T(w)可表示为:
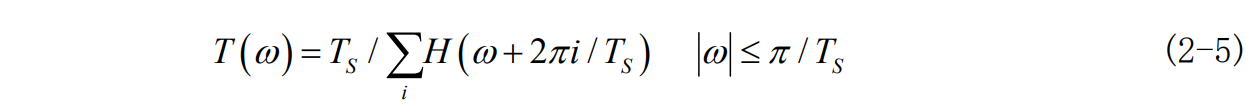
表示为傅里叶级数为:
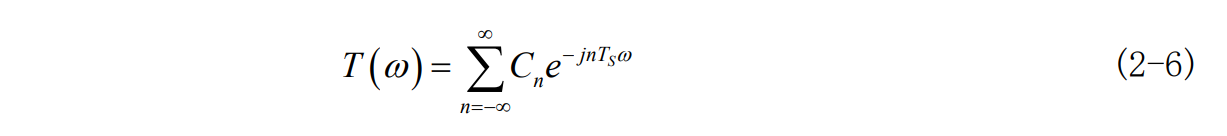
其中
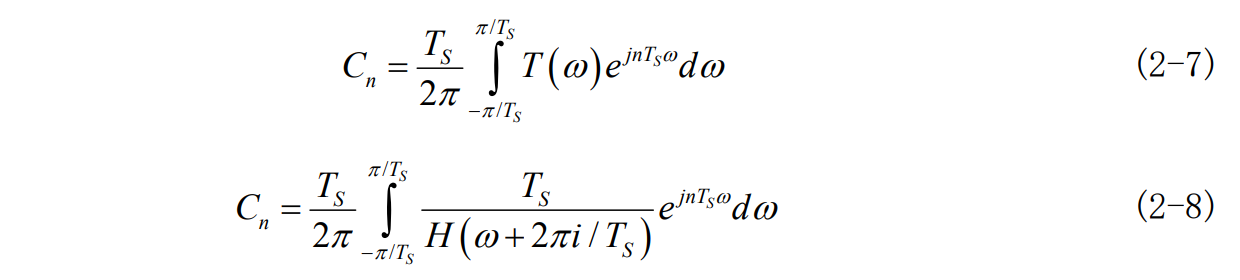
由式 2-8 可以看出傅里叶系数C_n由H(w)决定。对T(w)求傅里叶反变换,可得到其单位冲击响应:
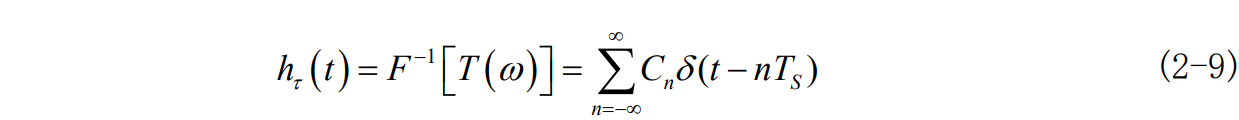
式 2-9 所示的滤波器可用下图 2-3 表示:
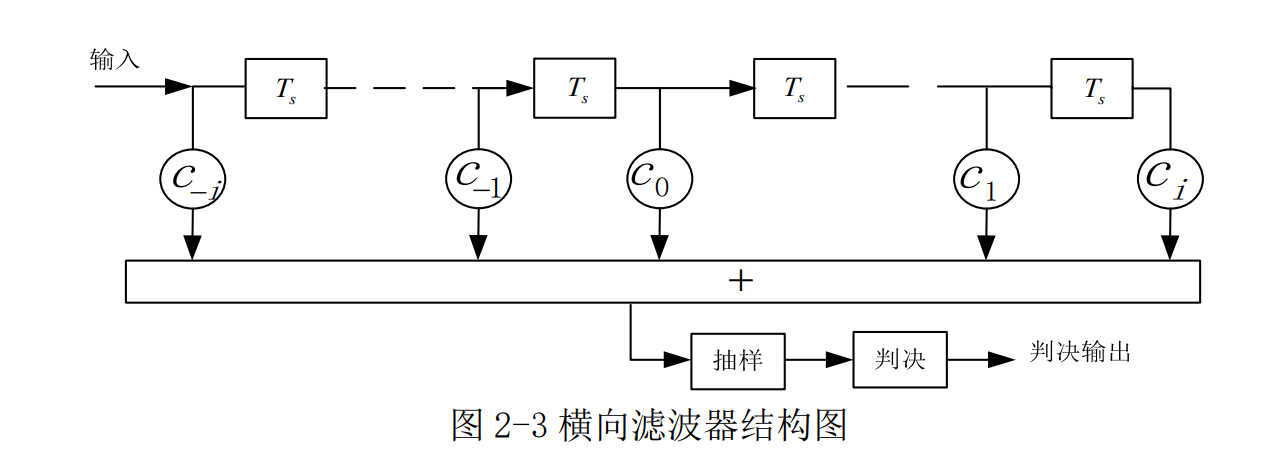
根据式 2-8 横向滤波器的特性取决于各抽头系数Cn。假设横向滤波器由 2N个延迟单元、2N+1 个抽头系数及一个加法器构成。由图 2-3 得到其单位冲击响应为:
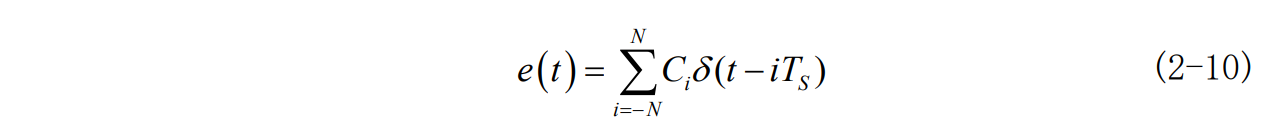
设系统无延时,在抽样时刻 t=kT_s上,有
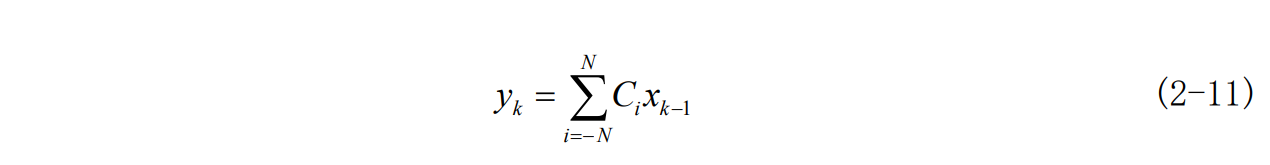
说明,均衡在第k个抽样时刻上得到的样值将由 2N+1 个C_i 与x_{k-1}的乘积之和来确定。当输入波形给定,同时要求y_k 都为 0 是几乎不能办到的。所以有限长的横向滤波器不可能完全消除码间串扰,此时需要考虑均衡需要达到的效果,因此建立均方失真准则和峰值失真准则来度量剩余失真的大小,以此来确定横向滤波器的抽头系数。此处仅考虑用最小峰值失真准则下的迫零算法来求横向滤波器的抽头系数。
3、迫零均衡算法
根据最小峰值失真准则,峰值失真表示为:
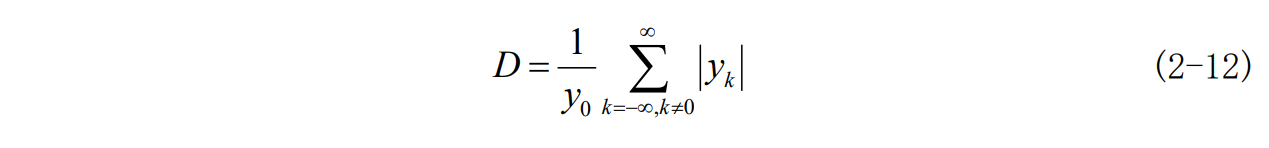
均衡前归一化峰值失真(初始失真),令y_0为 1,则:
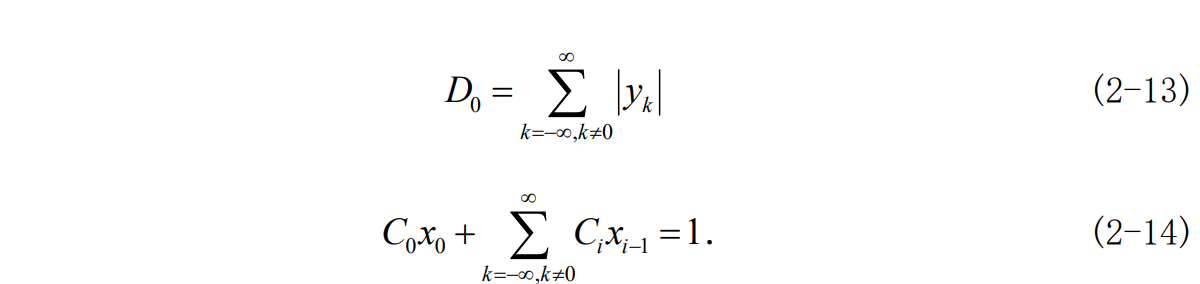
将式 2-14 带入式 2-11 可得
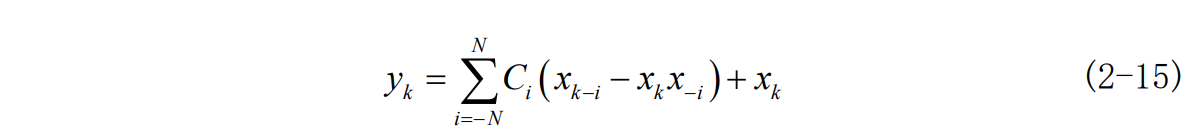
将式 2-15 代入式 2-12 则有:
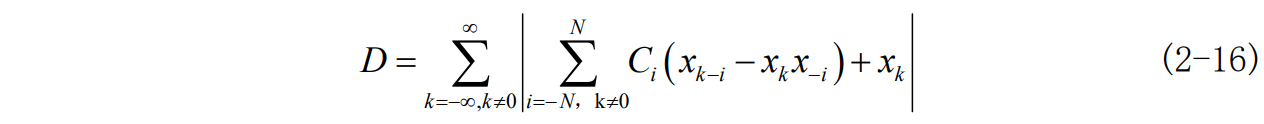
如果D_0 =1,峰值失真最小值一定发生在y_0前后的都等于y_k的情况。则无论采用什么方法求出的峰值失真最小值,一定是最终的峰值失真最小值
如果C_0可调,使y_0=1,则峰值失真是 2N 个C_i的凸函数。如果D_0=1,应调整抽头系数,使
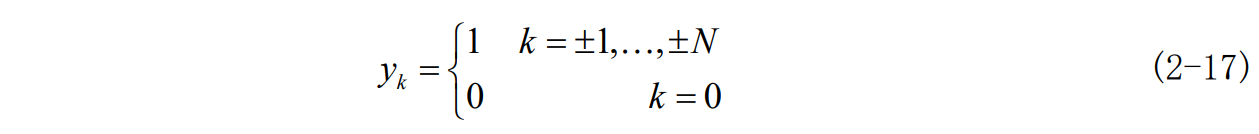
故所求的抽头系数C_i就是式 2-19 成立时2N+1个方程组成的方程组的解,下面详细说明迫零算法计算均衡器抽头系数的步骤。
根据图 2-1 中的通信系统模型,其冲激响应为
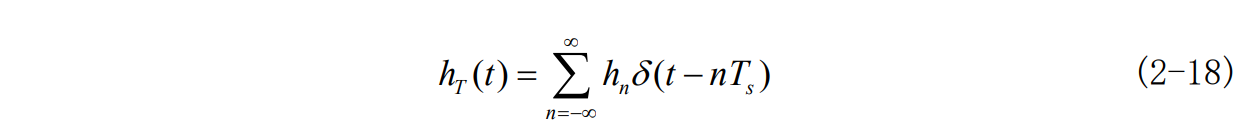
2N+1阶迫零均衡器的冲激响应为
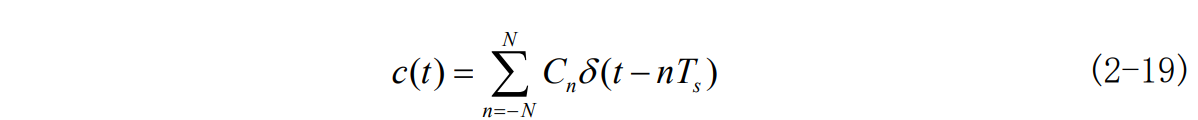
则其均衡器的抽头系数为
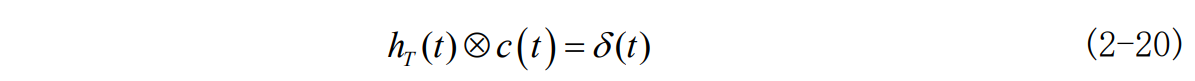
写成矩阵展开式如下:
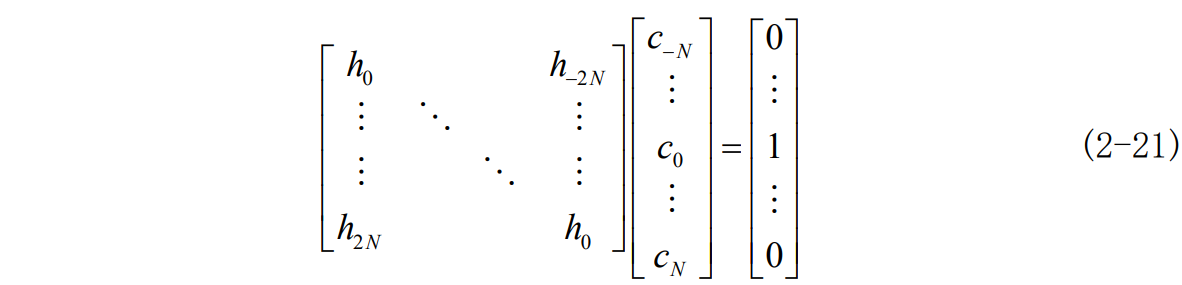
写成频域形式如下:
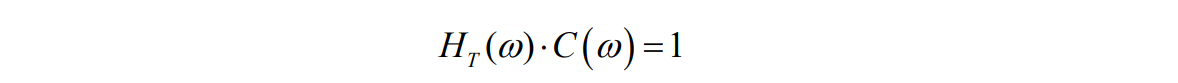
三、 实验仪器设备与材料
信号分布图
眼图
随机 M 进制序列模块
多径干扰模块
迫零均衡模块
四、 实验方法与步骤要求
1、如下图所示搭建仿真实验模型:对经多径干扰后的信号进行迫零均衡处理,仿真对比迫零均衡前后的信号的分布图及眼图变化。
搭建好的模型及整体界面如下图所示:
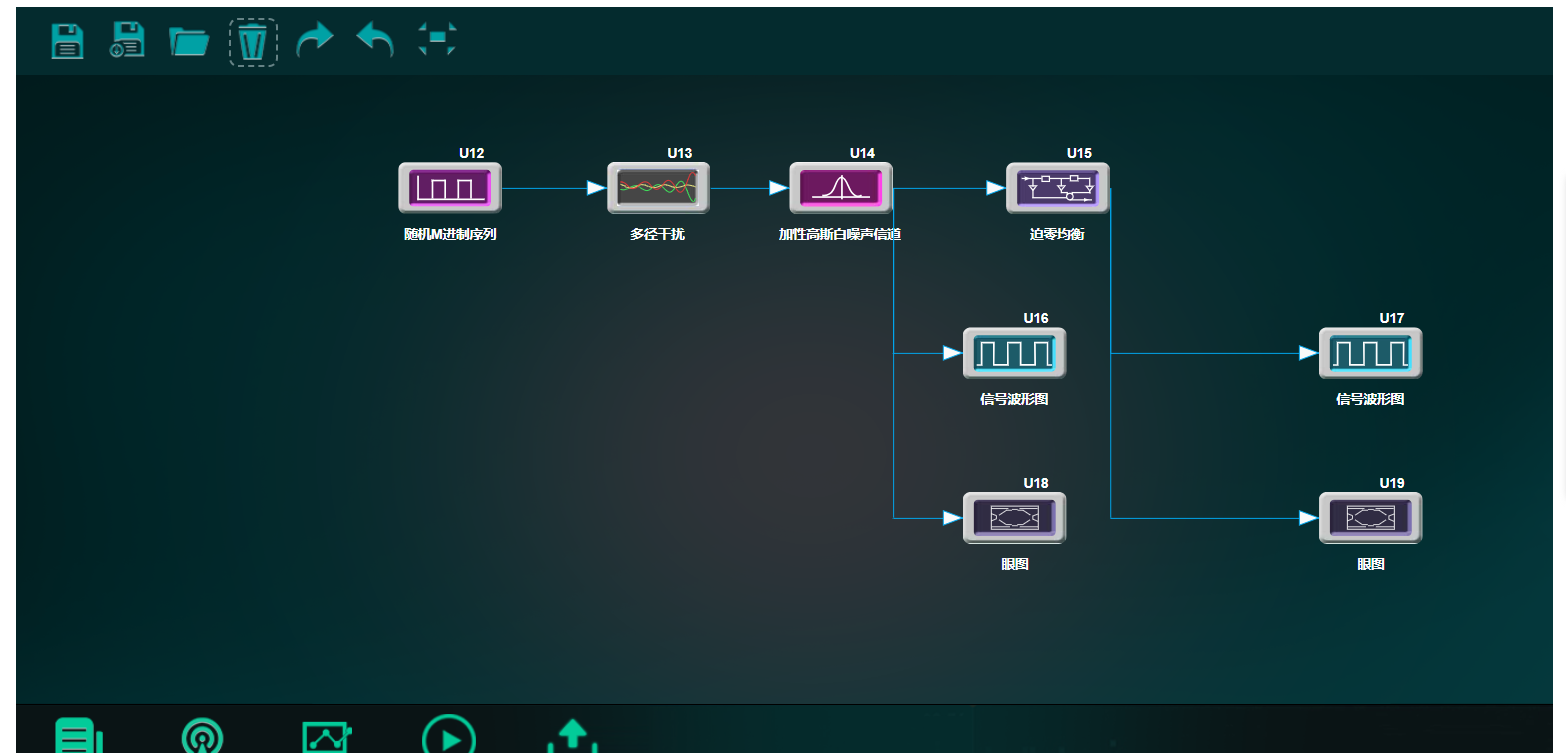
2、设置模块参数:(关于模块使用方法可以参考模块说明)
a.随机 M 进制序列模块:序列数据的长度(Length)设置为 1000,进制数(M)设置为 2;

b.多径干扰模块:多径信道的冲激响应(Multipaths)设置为[0.01 0.02 0.05 0.1 -0.2 1 -0.5 0.03 0.02];

c.加性高斯白噪声信道模块:设置(SNR)为 30dB
d.迫零均衡模块:多径信道的冲激响应(Multipaths)设置为[0.01 0.02 0.05 0.1 -0.2 1 -0.5 0.03 0.02],均衡器的抽头数(Tapnum)设置为 2;

e.眼图:每个轨迹的采样点数(Sampnum)设置为 2;

f.信号波形图:采用缺省设置。
3、点击按钮运行仿真实验,观察输出波形,测量眼图的眼高h_1。
4、将均衡器抽头数(Tapnum)修改为 9,保持其他模块参数不变,运行仿真实
验,观察输出波形,测量眼图的眼高h_2。
5、将均衡器抽头数(Tapnum)修改为 16,保持其他模块参数不变,运行仿真实验,观察输出波形,测量眼图的眼高h_3。
6、选做部分。根据最小二乘算法原理,自设训练序列\{t[0],t[1],……,t[N-1]\}完成均衡器的m代码,构造一个直接最小二乘均衡器,对比均衡前和均衡后的信号分布图和眼图,分析该算法的性能,并与迫零均衡算法进行对比分析,比较两种算法的优劣。
五、 实验结果与结论
采用上述设置的参数,运行信道均衡仿真实验,得到抽头数为 2 时迫零均衡前后的信号波形图及眼图,如图 2-12 和 2-13 所示。
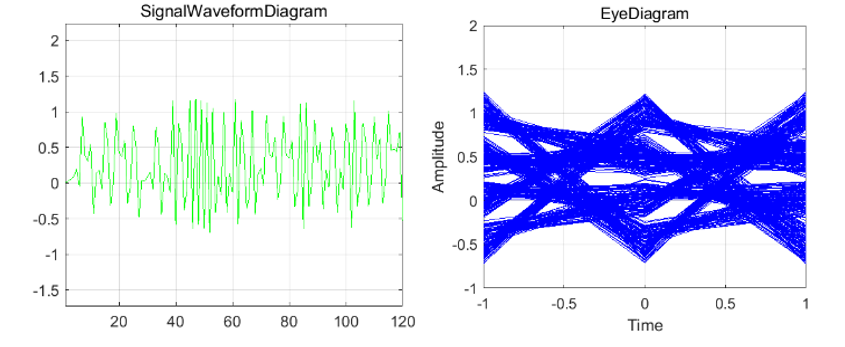
由仿真结果易知,经过多径信道后,信号产生了较严重的码间串扰,经过抽头数为 2 的迫零均衡器后,接收特性得到了一定的改善,但是接收眼图张开程度较小,仍然存在一定码间串扰。
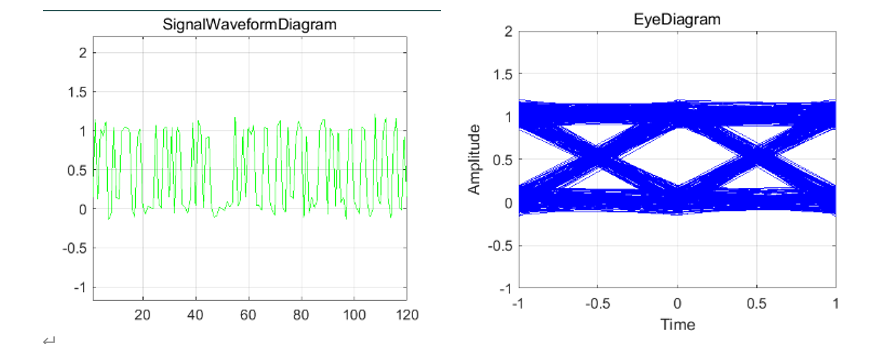
将均衡器抽头数修改为 9 后得到的均衡后信号波形图及眼图如图 2-14 所示。将仿真结果与图 2-13 对比易发现,均衡后的信号眼图高度h_2>h_1,眼图已经完全张开,易知 9 抽头均衡器的均衡效果比 2 抽头均衡器要好得多,信号接收特性得到了明显改善,信号的码间干扰得到了很大的改善。
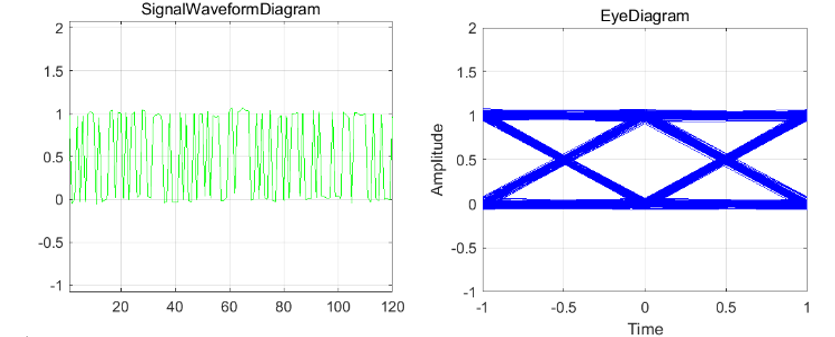
将均衡器抽头数修改为 16 后得到的均衡后信号分布图及眼图如图 2-15 所示。将仿真结果与图 2-14 对比易发现眼图张开程度比 9 抽头时略好,测量眼图高度可知h_3>h_2 ,但近似于h_2 \approx h_3 ,易知 16 抽头均衡器的均衡效果与 9 抽头均衡器相比,性能提升效果微乎其微。
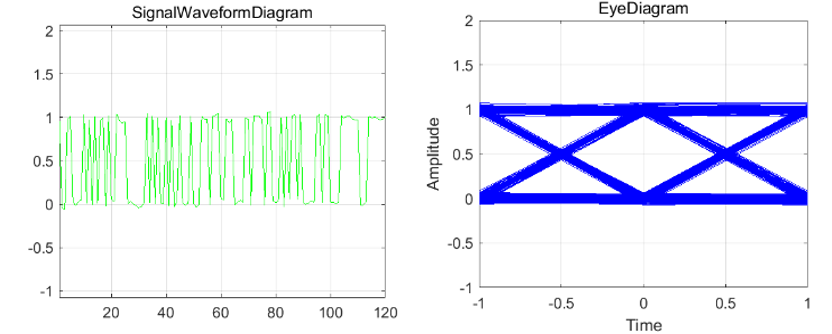
根据实验结果图可知用 N 阶迫零均衡器去均衡M径信道时,N越大,均衡效果越好;如果N<M,则均衡效果较差,误码率较高,增大 N对均衡效果改善较大;如果N\geq M ,则均衡效果较好,误码率较低,继续增大N对均衡效果改善不再明显。


